גרר הידרודינמי

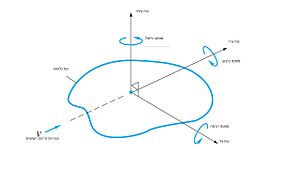
על כל גוף הנמצא בתוך זורם יחולו כוח גְּרָר הִידְרוֹדִינָמִי ומומנטים כתוצאה מהזרימה סביבו. גודל הכוח יהיה תלוי במהירות הזרימה יחסית ${\vec {U}}$, צורת הגוף ותכונות הזורם $\rho ,\mu$ וכדומה. אם לגוף צורה שרירותית, יחולו על הגוף מומנטים וכוחות בשלושת כיווני הצירים (ראו תמונה). נהוג לבחור בציר המקביל לכיוון החיובי של הזרימה כך שהכוח בכיוון ציר זה יכונה 'כוח גרר'.כוח זה מהווה בור אנרגטי בזרימה. המומנט בציר זה נקרא 'מומנט סיבוב'. כוח חשוב נוסף המאונך לכיוון הזרימה המשמש לנשיאת משקל הגוף, נקרא כוח עילוי. המומנט בציר זה נקרא 'מומנט פיתול'. מרכיב נוסף, הוא כוח צד. כוח זה אינו בור או מקור אנרגטי. המומנט בציר זה נקרא 'מומנט הרמה'. כאשר הגוף הנמצא בזרימה הוא סימטרי במישור העילוי-גרר, כדוגמה מטוס, רכב או אונייה, כוח הצד ומומנטי הסיבוב והפיתול נעלמים כך שהבעיה הופכת דו-ממדית: כוח עילוי, כוח גרר ומומנט הרמה.

תמונה א. תיאור כוח הגרר על גוף שרירותי

רקע פיזיקלי

כוח הגרר אינו מופיע בצורה מפורשת במשוואות נאוויה-סטוקס, אלא מתקבל מפתרון מלא שלהן (שדה המהירויות ושדה לחצים) כתוצאה מתנאי הגבול ${\vec {v}}=0$ (אי חדירה ואי החלקה על משטח הגוף). כלומר, כדי לקבל את ערך כוח הגרר האינטגרלי, יש לסכום את כל המאמצים (מאמצי הגזירה המשיקיים ומאמצי הלחץ המאונכים) על משטח הגוף בצורה הבאה,

$F_{D}=\iint _{S}P\cdot {\hat {n}}dS+\mu \iint _{S}\nabla (u)\cdot {\hat {n}}dS$

למשוואות נאוויה-סטוקס לא קיים פתרון כללי ידוע, אלא רק תחת הנחות מסוימות המאפשרות פתרונות עבור מקרים אחדים, ומכאן שלא ניתן למצוא את ערך כוח הגרר.

כאשר ניתן לעשות שימוש בהנחות סבירות למציאת שדה מהירויות ולחצים, בהינתן שהגוף עליו פועל כוח הגרר הוא מורכב גאומטרית (לדוגמה עלווה של עץ) תצריך מציאת ערך כוח הגרר כוח מחשוב אדיר. לפיכך, נוסחו במהלך ההיסטוריה של חקר הגרר, מספר מודלים שונים לביטוי הגרר על גופים שונים תחת תנאי זרימה שונים.

המודל הקלאסי

המודל הקלאסי אותו ניסח לורד ריילי (Rayleigh) מתאים לגופים הנמצאים תחת משטר זרימה בעל מספר ריינולדס, $Re\gg 1$ (כלומר, השפעות הצמיגות זניחות) נראה כך:

ערכים ספרותיים עבור מקדם כוח הגרר

$Drag=0.5\rho C_{D}AU^{2}$

ערכים אמפיריים עבור מקדם גרר כפונקציה של מספר ריינולדס. הקו המלא מייצג ספירה חלקה והקו השבור מייצג ספירה מחוספסת. המספרים לאורך הקווים מייצגים שינוי במשטר הזרימה והשינויים במקדם הגרר בהתאם. 2: זרימה צמודה (זרימת סטוקס) וזרימה מנותקת יציבה 3: זרימה מנותקת עם שכבת גבול למינרית במעלה ההיתנקות היוצרת שובל ערבולים סדורים. 4: זרימה מנותקת עם שיכבת גבול במעלה ההיתנתקות והזרימה בשובל היא טורבולנטית. 5: זרימה מנותקת על קריטית עם שכבת גבול טורבולנטית

כאשר, $\rho$ היא צפיפות הזורם, $U$ היא מהירות הזרימה ה"חופשית" (כלומר רחוק מהגוף עליו פועל הגרר), $C_{D}$ הוא מקדם הגרר (אופייני לכל צורה ותנאי זרימה) ו־$A$ הוא גודל גאומטרי המאפיין את הצורה.

בדרך־כלל הגודל $A$ הוא אחד משלושת הגדלים הבאים:

• שטח חתך המאונך לציר הזרימה (מתאים לגופים בעלי נפח כגון: גליל, כדור, כלי רכב, טילים)
• שטח הצורה ממבט על (מתאים לכנפיים של מטוס או ציפור)
• שטח פנים (מתאים לצורות מורכבות כגון עלוות עצים)

מקדם כוח הגרר

הבדלים ברורים בנקודות התנקות הזרימה מהכדור בין שכבת גבול למינרית (a) לשכבת גבול טורבולנטית (b) שנוצרה עקב הוספה של אזור מחוספס בקדמת הכדור

תמונה זו מוצגת בוויקיפדיה בשימוש הוגן.
נשמח להחליפה בתמונה חופשית.

בספרות קיים מספר רב של ערכים סמי-אנליטיים ואמפיריים עבור מקדם כוח הגרר תחת תנאי זרימה שונים וצורות הנדסיות שונות. מקדם הגרר מוגדר כיחס בין הפרשי הלחצים של הצורה (למשל לפני ואחרי הקוביה) לבין האנרגיה הקנטית (חצי המהירות בריבוע, שכאמור מורכבת מהמהירות הממוצעת והטורבולנטית). מקדמי הגרר המדוברים הם למעשה ממוצע מרחבי של מקדמי הגרר ולמעשה ללא המיצוע מקדם הגרר משתנה במרחב, לדוגמה מקדם הגרר במרכז הקוביה הוא שונה ממקדם הגרר בקצה הקוביה. נתבונן כדוגמה במקדם כוח הגרר על ספירה (ראה גרף א,). ניתן לראות בגרף א' את מקדם כוח הגרר כתלות במספר ריינולדס $Re$. במספרי ריינולדס נמוכים הזרימה מסביב לספירה אינה מתנתקת מפני השטח שלו, השובל הוא למינרי ורוב כוח הגרר נובע מחיכוך (ראה חוק סטוקס - במידע נוסף). ניתן להראות כי מקדם הגרר במשטר זרימה זה מתנהג לפי $C_{D}=24/Re$. (נשים לב כי כאשר $C_{D}\propto 1/Re$ אז $F_{D}\propto U$) ככל שעולה מספר ריינולדס עד לערך של $Re\cong 1000$, מקדם כוח הגרר יורד אך לא בקצב שמנבא חוק סטוקס. שובל טורבולנטי מתפתח וגדל בחלקה האחרי של הספירה בזמן שנקודת ההיפרדות של קווי הזרימה מפני שטח הכדור מתקדמת מחלקו האחורי לכיוון חלקו הקדמי. הלחץ בשובל נמוך יחסית ללחץ הנבנה בקדמת הספירה כך שב $Re\cong 1000$ 95% מכוח הגרר נובע מהפרשי לחצים. ב $10^{3}<Re<3\times 10^{5}$ מקדם כוח הגרר כמעט קבוע וכי בחלקה האחורי של הספירה ישנו שובל ערבולי. נשים לב כי כאשר $C_{D}\propto Const.$ אז $F_{D}\propto U^{2}$.

במספרי ריינולדס $Re>\backsim 3\times 10^{5}$, מתרחשת תופעת מעבר ושכבת הגבול על חלקה הקדמי של הספירה הופך טורבולנטי. נקודת ההיפרדות של קווי הזרימה נעה ממרכזו בכיוון מורד הזרימה על פני הכדור כך שאזור השובל קטן, הגרר נטו הפועל על הספירה קטן ומקדם הגרר יורד באופן פתאומי בהתאמה. מהירות הזרימה בה מתרחש מעבר זה תלויה בחיספוס הספירה (חספוס משטחים) ומאפייני הזרימה הפוגשת את הספירה. לדוגמה, תפקידן של הגומחות הקטנות שבפני כדור גולף הוא לגרום למעבר מהיר יותר לשכבת גבול עירבולית ובכך להוריד את הגרר הפועל על הכדור.

קישורים חיצוניים

מודלים למשטרי זרימה בהם ישנה חשיבות לצמיגות:

תנועת ספירה בתווך צמיג ובמספר ריינולדס $Re\ll 1$

• חוק סטוקס

סרטונים בנושא - National committee for fluid mechanics

• חלק ראשון
• חלק שני
• חלק שלישי
• חלק רביעי