מרחב ארבע-ממדי

מרחב ארבע-ממדי הוא מרחב שלו ארבעה ממדים. המונח מרחב ארבע-ממדי מציין ארבעה ממדים זהים בתכונותיהם. מספר עצמים תאורטיים נהגו בארבעה ממדים, בהם הכללות של עצמים משניים ושלושה ממדים: טסרקט הוא הכללה ארבע-ממדית של קובייה תלת־ממדית, כפי שקובייה היא הכללה של ריבוע דו-ממדי. המרחב מוצג באלגברה באמצעות וקטור ארבע-ממדי המציין מיקום במרחב. ניתן גם להציגו באמצעות הבסיס הסטנדרטי $(e1,e2,e3,e4)$, השווה למרחב $\mathbb {R} ^{4}$ ופורש אותו.

הדגמה כיצד מלבן בשלושה ממדים יראה במרחב 4 ממדים.

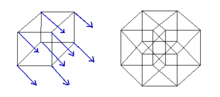
גדלים וצורות במרחב בעלי יותר משלושה ממדים מקבלים קידומת "היפר", כגון היפרספרה, היפרקובייה, היפרנפח, היפראליפסה. במרחב הארבע ממדי ישנם שישה גופים אפלטוניים, חמישה מהם גרסאות ארבע ממדיות של גופים אפלטוניים בתלת־ממד, ואחד מהם, ההיפרמעוין, הוא צורה חדשה.

בפיזיקה, בתורת היחסות, מתייחסים למרחב בעל 3+1 ממדים, בו שלושה מהממדים הם המרחב המוכר והממד הנותר מייצג את הזמן, ואינו מיוצג במשוואות בדיוק באותו אופן, ולכן הוא אינו מרחב ארבע-ממדי על פי ההגדרה. מיקום במרחב זה מיוצג באמצעות 4-וקטור, שהוא וקטור בעל ארבעה רכיבים, שהראשון שבהם מייצג את הזמן והיתר את המרחב התלת-ממדי.

לואיזה בונפיליולי הייתה בין המדענים הישראלים הראשונים שעסקו בתחום ובשנת 1966 זכתה בפרס של החברה אמריקאית להנדסה על מחקריה בתחום זה.

ראו גם

• קווטרניון (וקטור/מספר 4-ממדי):
  • אלגברת קווטרניונים
    • אלגברת הקווטרניונים של המילטון
• מרחב תלת-ממדי
• מרחב אוקלידי

לקריאה נוספת

• רודי רקר, הממד הרביעי - סיור מודרך ביקומים הגבוהים, הוצאת מאגנס

ערך זה הוא קצרמר בנושא מתמטיקה. אתם מוזמנים לתרום לוויקיפדיה ולהרחיב אותו.