מרחב פאזה
בפיזיקה, מרחב פאזה הוא מושג המשמש בעיקר לתיאור והבנה של מערכות דינאמיות. מרחב הפאזה הוא מרחב הפורש את כל המצבים האפשריים של מערכת פיזיקלית (באופן הרחב של המילה) ועל פי התנאים שהמערכת נתונה בהם ניתן לתאר מסלולים במרחב זה שלרוב מתארים את ההתנהגות המרחבית של מערכת פיזיקלית כלומר, מוצגים בעיקר ביחס למרחב (ולא לזמן), כך מרחב הפאזה מסוגל להרחיב לנו את האינטואיציה וההבנה לגבי ההתנהגות של המערכת וללמד אותנו תכונות נוספות החבויות בהתנהגות זו כאשר בוחנים אותם כתלות בזמן.

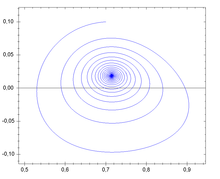
הגדרה
עריכהמרחב פאזה הוא מרחב רב-ממדי המהווה תיאור גאומטרי לכל מצב אפשרי של מערכת פיזיקלית. כל דרגת חופש של המערכת מיוצגת על ידי ציר במרחב הפאזה כך שכל נקודה במרחב הפאזה מגדירה את המצב של המערכת (כלומר קובעת פרמטר עבור כל דרגת חופש).
מקור והיסטוריה
עריכהמקור המושג של מרחב הפאזה קצת מעורפל וצף ככל הנראה במשך דורות, אך הוא הפך למרכזי בפיזיקה המודרנית באמצע המאה ה-19, עם ניסוחו של לודוויג בולצמן וג'יימס קלרק מקסוול למכניקה סטטיסטית, ניסוחו מחדש של המילטון למכניקה ומשפט ליוביל. המושג התחיל להשתרש בשפה המדעית בסוף המאה ה-19 בעבודתם של ג'וסיה וילארד גיבס והנרי פוינטקר.
מכניקה אנליטית
עריכהעל פי מכניקה אנליטית, ניתן לתאר מערכת פיזיקלית על ידי קואורדינטות מוכללות כך שלכל קואורדינטה מגדירים תנע צמוד (לדוגמה עבור מיקום בציר חד-ממדי התנע המוכלל יהיה התנע לאורך אותו הציר ועבור זווית התנע הצמוד יהיה התנע הזוויתי). עבור כל קואורדינטה מוכללת והתנע הצמוד שלה נפרש מרחב פאזה דו-ממדי עבור כל חלקיק. במערכת עם חלקיק אחד, כל נקודה במרחב הפאזה תציין את המיקום והתנע של החלקיק והמסלול של החלקיק יקבע על פי ההמילטוניאן של המערכת ותנאי ההתחלה. הפורמליזם ההמילטוני מגדיר את המילטוניאן ואת הבעיה הפיזיקלית כסט של משוואות דיפרנציאליות מסדר ראשון במרחב הפאזה.
מכניקה סטטיסטית
עריכהמכניקה סטטיסטית מתעסקת בספירה של מצבים. המצב של חלקיק נקודתי קלאסי מתואר באופן מלא על ידי המיקום והתנע שלו (מהירות כפול מסת החלקיק). למשל עבור מערכת תלת-ממדית המורכבת מ-N חלקיקים נקודתיים (חסרי ממדים), מרחב הפאזה יהיה בעל N6 ממדים – 3 ממדים עבור המיקום של כל חלקיק ו3 ממדים עבור התנע שלו. בעזרת מרחב הפאזה נוכל לתאר מצב של חלקיק כנקודה במרחב בעל 6 ממדים ומצבה של כלל מערכת תואם להתפלגות מסוימת של נקודות במרחב זה. כעת נוכל לדמיין את ספירת המצבים בצורה גאומטרית כנפח במרחב הפאזה.
אם נוסיף לכל חלקיק נפח כדורי אז יתווספו עוד 3 דרגות חופש עבור התנע הזוויתי, כלומר, סיבוב של החלקיק סביב כל אחד מהצירים המרחביים. לכן מרחב הפאזה כעת הוא בעל 9N ממדים כי כעת נצטרך 9 פרמטרים כדי לתאר את המצב של כל חלקיק.
בנוסף נבחין שעבור חלקיקים מובחנים, המצב המיקרוסקופי של המערכת (המיקומים והתנעים של כל החלקיקים) מוגדר על ידי נקודה במרחב זה. אם החלקיקים אינם מובחנים מצב מיקרוסקופי יכיל !N נקודות (בהתאם למספר האפשרויות שניתן לסדר את המערכת כך שלא נבחין בשינוי).
עקרון האי ודאות
עריכהספירת מספר המצבים הזמינים לחלקיק מסתכמת בקביעת הנפח הזמין במרחב הפאזה. אפשר לטעון כי עבור מרחב פאזה רציפה, כל נפח סופי יכיל מספר אינסופי של מצבים. אך עקרון האי-ודאות קובע כי לא ניתן לדעת במדויק את המיקום והתנע של חלקיק קוונטי כלומר לא ניתן לדעת בוודאות את המצב המלא של החלקיק לכן עבור חלקיק נקודתי יחיד בממד 1 במקום נקודה במרחב הפאזה המצב יתואר על ידי אלמנט נפח קטן כך שלפי העיקרון הנפח המינימלי שנוכל לקבל הוא
כאשר h הוא קבוע פלאנק.
מערכת מאקרוסקופית
עריכהמערכת תרמודינמית ניתנת לתיאור על ידי המשתנים התרמודינמיים שלה (אנרגיה, טמפרטורה, לחץ ועוד), עבור כל משתנה בלתי תלוי של המערכת נקבע ציר במרחב הפאזה ונקודה במרחב זה תקבע המצב המאקרוסקופי של המערכת. דיאגרמת פאזות המתארת מעברי פאזה של חומרים היא מקרה פרטי של מרחב פאזה של מערכת מאקרוסקופית עבור משתנים תרמודינמיים מסוימים. ישנם כמה מצבים מיקרוסקופיים המתאימים למצב מקרוסקופי מסוים לכן מבחינה טופולוגית מרחב הפאזה המיקרוסקופי מהווה יריעה מממד גבוה יותר של מרחב הפאזה המאקרוסקופי.
ראו גם
עריכהשימושים
לקריאה נוספת
עריכה- The Tangled Tale of Phase Space", (2010), David D. Nolte"
- The Explanatory Power of Phase Spaces", (2007), A. Lyon and M.Colyvan"