מרחב קשיר מקומית

מרחב קשיר מקומית בטופולוגיה, ובתחומים מתמטיים נוספים, הוא מרחב טופולוגי שבו כל סביבה של נקודה מכילה סביבה פתוחה וקשירה. תכונת הקשירות המקומית קרובה באופייה לתכונת הקשירות, אבל השתיים אינן גוררות זו את זו.

רקע

קשירות וקומפקטיות הן שתי תכונות בסיסיות בטופולוגיה. חשיבותן של תכונות אלה הוכרה בתחילה עבור תת-קבוצות של המרחב האוקלידי, אלא שעד מהרה הוברר שהתכונות אינן תלויות במטריקה המוגדרת על המרחב, אלא במאפיינים הטופולוגיים שלו.

מרחב המסרק, המוגדר על ידי איחוד של ציר x עם קווים המקבילים לציר y במרחק

1/n

הוא קשיר מסילתית, אך אינו קשיר מקומית סביב הנקודה המסומנת

משפט היינה-בורל, ומשפטים חזקים נוספים, מאפשרים לתאר את הקבוצות הקומפקטיות במרחב האוקלידי. אפילו במקרה זה, המבנה של קבוצות קשירות מורכב יותר. לדוגמה, כל מרחב האוסדורף קומפקטי הוא קומפקטי מקומית, ועם זאת, מרחב קשיר אינו חייב להיות קשיר מקומית, אפילו אם מדובר על תת-מרחב של המרחב האוקלידי (ראו מרחב המסרק באיור משמאל).

הגדרות ותכונות בסיסיות

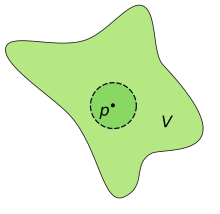
מרחב טופולוגי $X$ הוא קשיר מקומית בנקודה $x$ , אם לכל קבוצה פתוחה $V$ המכילה את $x$ , קיימת תת-קבוצה קשירה ופתוחה $U$ עבורה $x\in U\subset V$ . מרחב שהוא קשיר מקומית בכל נקודה הוא מרחב קשיר מקומית^[1].

אם לכל קבוצה פתוחה $V$ המכילה את $x$ קיימת קבוצה פתוחה וקשירה $N\subset V$ כך ש- $x$ נמצא בפנים של $N$ , אומרים ש- $X$ קשיר מקומית באופן חלש ב- $x$ .^[2]. המרחב קשיר מקומית בנקודה $x$ אם יש לו בסיס מקומי של קבוצות פתוחות וקשירות, וקשיר מקומית באופן חלש, אם יש לו שם בסיס מקומי של סביבות קשירות (כל קבוצה פתוחה הכוללת את הנקודה היא סביבה שלה, אבל ההפך אינו נכון). מכאן שאם המרחב קשיר מקומית בנקודה, הוא גם קשיר שם מקומית באופן חלש. ההפך אינו נכון, ועם זאת, מרחב שהוא קשיר מקומית באופן חלש בכל נקודה שלו, הוא בהכרח קשיר מקומית בכל נקודה.^[3]

כל מרחב קשיר מסילתית הוא קשיר, ולכן מרחב קשיר מסילתית מקומית הוא גם קשיר מקומית.

דוגמאות

לכל מספר טבעי $n$ , המרחב האוקלידי $\mathbb {R} ^{n}$ קשיר וקשיר מקומית.
המרחב $[0,1]\cup [2,3]$ קשיר מקומית, איך אינו קשיר.
המרחב $\{(x,\sin {\frac {1}{x}})|x\in (0,\infty )\}\cup \{0\}\times [0,1]$ (הידוע כ"עקומת הסינוס של הטופולוגים") קשיר, אך אינו קשיר מקומית ואינו קשיר מסילתית.^[4]
מרחב המספרים הרציונליים $\mathbb {Q}$ , עם הטופולוגיה המושרית מן הישר הממשי, אינו קשיר ואינו קשיר מקומית.
מרחב המסרק (ראו תמונה למעלה) קשיר וקשיר מסילתית אך אינו קשיר מקומית.
תהי $X$ קבוצה אינסופית בת מנייה. תחת הטופולוגיה הקו-סופית מתקיים כי $X$ קשירה מקומית אך לא קשירה מסילתית מקומית.^[5]

תכונות נוספות

על פי ההגדרה, קשירות מקומית היא תכונה מקומית. עם זאת, כל התכונות המתקיימות במרחב קשיר מתקיימות באופן מקומי במרחב קשיר מקומית, למשל:

מרחב הוא קשיר מקומית אם ורק אם קיים לו בסיס המכיל רק קבוצות קשירות.
איחוד זר של מרחבים הוא קשיר מקומית אם ורק אם כל אחד מהמאוחדים קשיר מקומית. בפרט, היות שמרחב הנקודה קשיר מקומית, כל מרחב דיסקרטי הוא קשיר מקומית. מצד שני, מרחב דיסקרטי הוא בלתי קשיר לחלוטין ועל כן הוא קשיר אם ורק אם יש בו לכל היותר נקודה אחת.
מרחב בלתי קשיר לחלוטין יהיה קשיר מקומית אם ורק אם הוא דיסקרטי. מכאן נובעת באופן מיידי הטענה בדוגמאות לפיה המספרים הרציונליים אינם מהווים מרחב קשיר מקומית.

רכיבי קשירות

ההגדרות המובאות בחלק זה מבוססות על התוצאה הבאה:

למה: תהי

\{Y_{\alpha }\}_{\alpha \in I}

משפחה של תת-קבוצות במרחב טופולוגי $X$ , שהחיתוך של כולן אינו ריק. אם כל קבוצה

Y_{\alpha }

קשירה (קשירה מסילתית) אזי האיחוד

\bigcup _{\alpha \in I}Y_{\alpha }

קשיר (קשיר מסילתית)^[6].

עתה נוכל לדון ביחס השקילות המוגדר כך ש- $x\equiv y$ אם קיימת תת-קבוצה קשירה של $X$ המכילה את $x$ ואת $y$ . ברור כי היחס הזה רפלקסיבי וסימטרי, והטרנזיטיביות שלו נובעת מהלמה. מחלקות השקילות של היחס נקראות רכיבי הקשירות של $X$ . מחלקת השקילות המכילה את $x$ נקראת רכיב הקשירות של $x$ ונהוג לסמנה על ידי $C_{x}$ .

מהלמה נובע כי רכיב הקשירות של $x$ הוא תת-הקבוצה הקשירה המקסימלית המכילה את $x$ . היות שהסגור של $C_{x}$ הוא קבוצה קשירה, ניתן להסיק שכל רכיבי הקשירות סגורים ב- $X$ .

אם למרחב $X$ יש מספר סופי של רכיבי קשירות, אזי כל רכיב קשירות הוא המשלים של איחוד סופי של קבוצות סגורות ועל כן פתוח בעצמו. באופן כללי רכיבי קשירות אינם מוכרחים להיות פתוחים (לדוגמה ניתן לקחת את מרחב קנטור, שהוא מרחב בלתי קשיר לחלוטין אך אינו מרחב דיסקרטי). עם זאת, רכיבי הקשירות של מרחב קשיר מקומי הם פתוחים. מכאן מתקבל שמרחב קשיר מקומית $X$ שווה לאיחוד רכיבי הקשירות שלו. מצד שני, אם לכל קבוצה סופית $U$ של $X$ מתקיים שרכיבי הקשירות של $U$ פתוחים, אזי ל- $X$ בסיס של קבוצות קשירות ולכן קשיר מקומית^[7].

דוגמה: הקבוצה $I\times I$ כאשר $I=[0,1]$ , ביחד עם טופולוגיית הסדר המושרית מיחס הסדר הלקסיקוגרפי היא בעלת רכיב קשירות אחד (כי היא קשירה). עם זאת, כל קבוצה מהצורה $a\times I$ מהווה רכיב קשירות מסילתית.

רכיבי קשירות של מרחב קשיר מקומית

טענה: בהינתן

X

מרחב קשיר מקומית, כל רכיבי הקשירות שלו פתוחים.^[8]

הוכחה: יהי

X

מרחב קשיר מקומית ויהי

C

רכיב קשירות. לכל

x\in X

יש קבוצה פתוחה קשירה

U_{x}

כך ש-

x\in U_{x}

וגם

C\subset U_{x}

. לכן:

C=\bigcup _{x\in C}U_{x}

ומכאן

C

פתוחה כאיחוד פתוחות.

מקורות

John L. Kelley; General Topology; ISBN 0-387-90125-6
Munkres, James (1999), Topology (2nd ed.), Prentice Hall, ISBN 0-13-181629-2
Stephen Willard; General Topology; Dover Publications, 2004.

ראו גם

קישורים חיצוניים

מרחב קשיר מקומית, באתר MathWorld (באנגלית)

הערות שוליים

^ Willard, Definition 27.4, p. 199
^ Willard, Definition 27.14, p. 201
^ Willard, Theorem 27.16, p. 201
^ Steen & Seebach, pp. 137–138
^ Steen & Seebach, pp. 49–50
^ Willard, Theorem 26.7a, p. 192
^ Willard, Theorem 27.9, p. 200
^ Willard, Corollary 27.10, p. 200

[1] Willard, Definition 27.4, p. 199

[2] Willard, Definition 27.14, p. 201

[3] Willard, Theorem 27.16, p. 201

[Steen-4] Steen & Seebach, pp. 137–138

[5] Steen & Seebach, pp. 49–50

[6] Willard, Theorem 26.7a, p. 192

[7] Willard, Theorem 27.9, p. 200

[8] Willard, Corollary 27.10, p. 200

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]