עץ פורש מינימלי

עץ פורשׂ מינימלי (באנגלית: Minimum spanning tree) של גרף ממושקל לא מכוון הוא עץ פורש (כלומר, תת-גרף קשיר ונטול מעגלים המכיל את כל הצמתים בגרף), שהוא מינימלי בסכום משקלי הקשתות שלו מבין כל העצים הפורשים.

בכתיב פורמלי: אם משקל הקשת $\ (u,v)$ הוא $w(u,v)$ ועבור עץ $T$ יהי משקלו $w(T)=\sum _{(u,v)\in T}w(u,v)$, העץ הפורש המינימלי הוא זה בעל $w\left(T\right)$ הקטן ביותר.

המחשה

חברת טלוויזיה בכבלים מניחה תשתית כבלים בשכונה כלשהי. אם החברה מוגבלת בכך שעליה להניח את הכבלים אך ורק לאורך מסלולים מסוימים, אזי יהיה גרף אשר מייצג את הנקודות המחוברות במסלולים אלו. חלק מן הקווים יכולים להיות יקרים יותר, מכיוון שהמרחק גדול יותר, או שיש צורך לקבור את הכבל עמוק יותר באזור זה.

עץ פורש של גרף זה הוא קבוצה חלקית הכוללת רק את המסלולים שאינם סגורים במעגל, ועדיין כל בית יהיה מחובר לתשתית הכבלים. לכל גרף (שאינו עץ) יש עצים פורשים רבים: ראו נוסחת קיילי ומשפט קירכהוף. עץ פורש מינימלי הוא עץ פורש בעל משקל כולל נמוך ביותר. יכולים להיות מספר עצים פורשים מינימליים.

תכונות

ריבוי אפשרי

דוגמה לגרף ממושקל (למעלה) עם יותר מעץ פורש מינימלי אחד

אם בגרף n קודקודים, אזי לכל עץ פורש n − 1 קשתות.

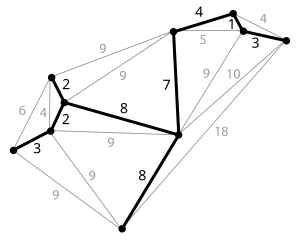
האיור מראה שיכול להיות יותר מעץ פורש מינימלי אחד בגרף. באיור, שני העצים מתחת לגרף הם שתי אפשרויות של עץ פורש מינימלי של הגרף הנתון עם משקל כולל 16.

ייתכנו מספר עצים מינימליים בעלי אותו משקל; בפרט, אם כל משקלי הקשתות של גרף נתון זהים, אז כל עץ פורש של הגרף הזה הוא מינימלי.

יחידות

אם לכל קשת בגרף משקל ייחודי אזי קיים עץ פורש מינימלי אחד בלבד. תכונה זו מתקיימת לעיתים קרובות במצבים מציאותיים, כמו למשל בדוגמה של חברת התקשורת לעיל, שם לא סביר ששני נתיבים יהיו בעלי אותה עלות בדיוק.

הוכחה

1. בדרך השלילה: נניח שקיימים שני עצים פורשים מינימליים A ו-B.
2. מכיוון ש-A ו-B שונים, למרות שהם כוללים אותם צמתים, קיימת קשת אחת או יותר ששייכת לעץ פורש מינימלי אחד אך לא לאחר. מבין הקשתות הללו, תהי $e_{1}$ הקשת בעלת המשקל הנמוך ביותר; בחירה זו היא ייחודית מכיוון שכל משקלי הקשתות שונים. ללא הגבלת הכלליות, נניח ש-$e_{1}$ נמצאת ב-A.
3. מכיוון ש-B הוא עץ פורש מינימלי $B\cup e_{1}$ חייב להכיל מעגל C, הכולל את $e_{1}$.
4. A הוא עץ ולכן אינו מכיל מעגלים, לכן C חייב לכלול קשת $e_{2}$ שאינה ב A.
5. מאחר שהקשת $e_{1}$ נבחרה כקשת בעלת המשקל הנמוך ביותר מבין הקשתות השייכות בדיוק לאחד מ-A ו-B, המשקל של $e_{2}$ חייב להיות גדול מהמשקל של $e_{1}$.
6. כיוון שהקשתות $e_{1}$ ו-$e_{2}$ הן חלק מהמעגל C, החלפת $e_{2}$ ב-$e_{1}$ ב-B יוצרת עץ פורש עם משקל קטן יותר, בניגוד להנחה ש-B הוא עץ פורש מינימלי.

במקרה כללי, כאשר לחלק מהקשתות בגרף משקלים זהים, ייתכנו מספר עצים פורשים מינימליים. אבל קבוצת (או מולטי-קבוצת) המשקלות בכל העצים הפורשים המינימליים תהיה זהה.

גרף הכולל מעגלים

אם המשקל של קשת $e$ במעגל כלשהו C בגרף גדול מהמשקלות של שאר כל שאר הקשתות של C, אז קשת זו אינה שייכת לאף עץ פורשת מינימלי.

הוכחה

בדרך השלילה. נניח כי הקשת $e$ שייכת לעץ פורש מינימלי $T_{1}$. מחיקת הקשת $e$ תפרק את $T_{1}$ לשני תתי-עצים כך ששני הקצוות של $e$ בתתי-עצים שונים. שאר הקשתות במעגל C מחברות מחדש את תת-העצים, מכאן שיש קשת $f$ ב-C עם קצוות בתתי-עצים שונים, כלומר, היא מחברת מחדש את תתי-העצים לעץ פורש $T_{2}$. ומכיוון שהמשקל של $f$ קטן מהמשקל של $e$ שסכום משקלות הקשתות של $T_{2}$ קטן מזה של $T_{1}$ בניגוד להנחה.

התפתחות האלגוריתם

האלגוריתם הראשון למציאת עץ פורש מינימלי בגרף לא מכוון הומצא בידי המדען הצ'כי אוטקר בוהרובקה ב-1926. מטרתו הייתה מציאת כיסוי חשמלי יעיל של חבל מוראביה. כיום משתמשים בשני אלגוריתמים ידועים לגרף לא מכוון: האלגוריתם של פרים והאלגוריתם של קרוסקל. שניהם אלגוריתמים חמדניים. שניהם רצים בזמן פולינומי, כך שמציאת פתרונות לבעיות כאלו, הם בתחום הסיבוכיות של P. זמן הריצה המדויק שלהם תלוי במבני הנתונים בהם משתמשים (לדוגמה ערימת פיבונאצ'י).

הניסיון למצוא את האלגוריתם המהיר ביותר לפתרון בעיה זו הוא מהוותיקים ביותר בתחום מדעי המחשב. אם משקלי הקשתות הם מספרים שלמים המוגבלים במספר הביטים המייצגים אותם, אזי ידועים אלגוריתמים מוחלטים (דטרמיניסטיים - שאינם פועלים באקראיות) עם זמן ריצה ליניארי $\ O(m)$. עבור משקלים כלליים, ידועים אלגוריתמים אקראיים הרצים בזמן שתוחלתו ליניארית במספר הקשתות.

האלגוריתם המהיר ביותר עד היום, לעץ פורש מינימלי, פותח על ידי ברנרד שאזל, ומבוסס על האלגוריתם של בוהרובקה. זמן הריצה שלו הוא: $\ O(m\alpha (m,n))$ כש-$\ m$ מסמן את מספר הקשתות, $\ n$ מסמן את מספר הצמתים ו-$\alpha (m,n)=\min\{i\geq 1:A(i,\lfloor m/n\rfloor )\geq \log _{2}n\}$ היא פונקציית אקרמן ההפוכה. קיומו של אלגוריתם דטרמיניסטי למשקלים כלליים, בעל זמן ריצה ליניארי עדיין נותר בגדר שאלה פתוחה.

ראו גם

• תורת הגרפים

קישורים חיצוניים

• עץ פורש מינימלי, באתר MathWorld (באנגלית)

• Otakar Boruvka on Minimum Spanning Tree Problem (translation of the both 1926 papers, comments, history) (2000) Jaroslav Nesetril, Eva Milková, Helena Nesetrilová (section 7 gives his algorithm, which looks like a cross between Prim's and Kruskal's)
• A Minimum Spanning Tree Algorithm with Inverse-Ackermann Type Complexity, Bernard Chazelle, 1999