פונקציה חלקית
פונקציה שתחום ההגדרה בפועל שלה עשוי להיות קטן מקבוצת הקלט שלה
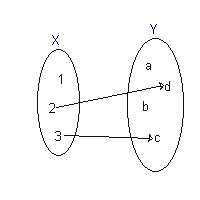
במתמטיקה, פונקציה חלקית (באנגלית: Partial function) מתחום לטווח היא יחס בינארי בין ל-, המקיים את התנאי של "חד ערכיות", כלומר: לכל איבר בקבוצה X קיים לכל היותר איבר אחד בקבוצה כך שהזוג שייך ליחס. אם לכל איבר בתחום קיים בדיוק איבר אחד בטווח כך שהזוג שייך ליחס, אז היא נקראת פונקציה שלמה, או בפשטות: "פונקציה".
לדוגמה, מ- ל- היא פונקציה חלקית, כי התחום שלה מכיל את כל המספרים השליליים, אשר לא מוגדרים עבור פוקנציית השורש הריבועי. לכן אינה פונקציה שלמה. אולם מ- ל- היא פונקציה שלמה, כיוון שהיא מוגדרת לכל ששייך ל-.
קישורים חיצוניים
עריכה- פונקציה חלקית, באתר MathWorld (באנגלית)








