קיטוב ליניארי

באלקטרודינמיקה, קיטוב ליניארי (ולפעמים "קיטוב מישורי") של הקרינה האלקטרומגנטית היא הגבלה של וקטור השדה החשמלי או המגנטי למישור נתון לאורך כיוון ההתפשטות. (ראו קיטוב למידע נוסף).

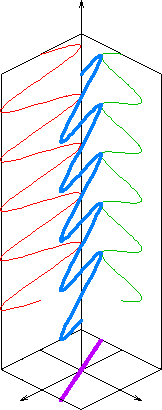
תרשים של השדה החשמלי של הגל (כחול), מקוטב ליניארית לאורך מישור (קו סגול), המורכב משני רכיבים (אדום וירוק)

הכיוון של גל אלקטרומגנטי מקוטב ליניארית מוגדר על ידי הכיוון של וקטור השדה החשמלי. לדוגמה, אם וקטור השדה החשמלי הוא אנכי (לסירוגין מעלה ומטה לאורך התקדמות הגל) נאמר כי הקרינה מקוטבת בקיטוב אנכי.

תיאור מתמטי של קיטוב ליניארי

הפתרונות הקלאסיים של משוואת גל סינוס מישורי אלקטרומגנטי עבור השדה החשמלי והמגנטי (ביחידות cgs)

$\mathbf {E} (\mathbf {r} ,t)=\mid \mathbf {E} \mid \mathrm {Re} \left\{|\psi \rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}$

$\mathbf {B} (\mathbf {r} ,t)={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)/c$

עבור השדה המגנטי, שבו k הוא מספר הגל,

$\omega _{}^{}=ck$

הוא התדר הזוויתי של הגל ו-c היא מהירות האור.

כאן $\mid \mathbf {E} \mid$ היא המשרעת של השדה.

$|\psi \rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}\psi _{x}\\\psi _{y}\end{pmatrix}}={\begin{pmatrix}\cos \theta \exp \left(i\alpha _{x}\right)\\\sin \theta \exp \left(i\alpha _{y}\right)\end{pmatrix}}$

הוא וקטור ג'ונס במישור x-y.

הגל מקוטב ליניארית כאשר זוויות הפאזה $\alpha _{x}^{},\alpha _{y}$ שווים,

$\alpha _{x}=\alpha _{y}\ {\stackrel {\mathrm {def} }{=}}\ \alpha$.

זה מייצג גל מקוטב בזווית $\theta$ ביחס לציר ה-x. במקרה זה, וקטור ג'ונס יכול להיכתב כ:

$|\psi \rangle ={\begin{pmatrix}\cos \theta \\\sin \theta \end{pmatrix}}\exp \left(i\alpha \right)$.

וקטורי המצב עבור קיטוב ליניארי ב-x או y הם מקרים מיוחדים של וקטור מצב זה.

אם וקטורי יחידה מוגדרים כך:

$|x\rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}1\\0\end{pmatrix}}$

וגם

$|y\rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}0\\1\end{pmatrix}}$

אז מצב ניתן להכתב בבסיס "x-y" כ:

$|\psi \rangle =\cos \theta \exp \left(i\alpha \right)|x\rangle +\sin \theta \exp \left(i\alpha \right)|y\rangle =\psi _{x}|x\rangle +\psi _{y}|y\rangle$.

ראו גם

• קיטוב מעגלי

קישורים חיצוניים

מדיה וקבצים בנושא קיטוב בוויקישיתוף

• אנימציה של קיטוב לינארי (ב-YouTube), סרטון באתר יוטיוב
• השוואה של קיטוב לינארי עם קיטובים מעגלי ואליפטי  (YouTube אנימציה), סרטון באתר יוטיוב
• מאמר זה משלב יצירה של הממשל הפדרלי של ארצות הברית ממסמך של "General Services Administration"‏ - "Federal Standard 1037C"^{[דרושה הבהרה]}