תרשים עץ (הסתברות)
בתורת ההסתברות, ניתן להשתמש בתרשים עץ (דיאגרמת עץ) כדי לייצג מרחב הסתברות.
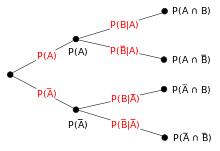
תרשימי עץ עשויים לייצג סדרה של מאורעות בלתי תלויים (כגון סדרה של הטלות מטבע) או מאורעות בעלי הסתברויות מותנות (כגון הוצאת כדורים משק). כל צומת בתרשים מייצג מאורע וההסתברויות שלהן זהות. צומת הגזע (הצומת הראשון) מייצג מאורע ודאי. כל קבוצה של צומתי אחים מייצגת חלוקה בלעדית וממצה של מאורע ההורה.
הסתברותו של צומת שווה להסתברות המאורע אליו הוא מקושר, לאחר שמאורע ההורה התרחש. ההסתברות שסדרת מאורעות המובילה לצומת מסוים תתרחש שווה למכפלת הסתברויות הצומת וכל הוריו.
למשל, אם יש כד עם 3 כדורים שחורים ו-2 כדורים לבנים, ואני מוציא שני כדורים בזה אחר זה- בלי להחזיר את הכדור הראשון שהוצאתי. אז הצומת הראשונה היא הוצאת הכדור הראשון - וההסתברות להוצאת כדור שחור היא 0.6 לעומת ההסתברות להוצאת כדור לבן שהיא 0.4. אם הוצאתי כדור שחור אז בצומת השנייה יש לי סיכוי של 0.5 להוצאת כדור שחור, והסתברות של 0.5 להוצאת כדור לבן (כיון שנותרו בכד 2 כדורים שחורים ו-2 כדורים לבנים). אולם, אם הוצאתי כדור לבן בתחילה - אזי בצומת השנייה יש לי סיכוי של 0.75 להוצאת כדור שחור, ו-0.25 להוצאת כדור לבן (כיון שנותרו בכד 3 כדורים שחורים וכדור אחד לבן). המשמעות של זה היא שההסתברות להוצאת שני כדורים שחורים למשל היא מכפלה של ההסתברויות 0.6 ו-0.5, כלומר 0.3. לעומת זאת ההסתברות להוצאת שני כדורים לבנים היא מכפלת ההסתברויות 0.4 ו-0.25, כלומר 0.1.

