טור פורייה

טוּר פוּרְיֶה הוא טור (סופי או אינסופי) של פונקציות מחזוריות, שמטרתו לקרב פונקציה נתונה. באופן עקרוני, טור פורייה הוא דרך לתאר כל סוג של פונקציה מחזורית ואת ההרמוניות שלה (שהן אותה פונקציה בסיסית עם תדר הולך וגדל) בעזרת חיבור של פונקציות טריגונומטריות בסיסיות (סינוס וקוסינוס). שיטה זו פותחה על-ידי המתמטיקאי הצרפתי ז'אן-בטיסט ז'וזף פורייה, והיא קרויה על שמו.

הרכבה של פונקציה מפונקציה מחזורית והרמוניות

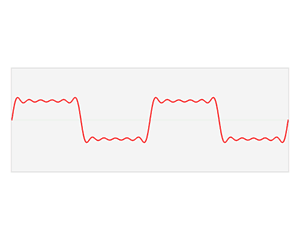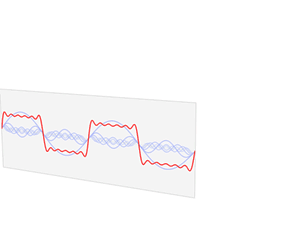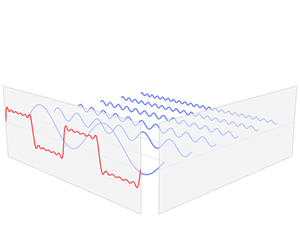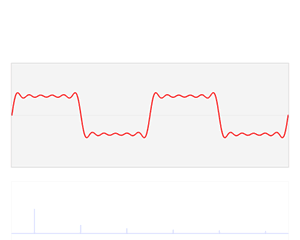
ניתן להוכיח שאפשר להציג כל פונקציה חלקה מספיק כסכום (ליתר דיוק, טור) של הרמוניות. המרה כזו של פונקציה נקראת פירוק פורייה, והסכום שנוצר נקרא טור פורייה. המרה זו היא שימושית ביותר בתחומים רבים כגון פיזיקה והנדסת אלקטרוניקה, והיא הכלי העיקרי לעיבוד תמונות ועיבוד אודיו.

במתמטיקה, לעיתים קרובות נוח להציג פונקציה מסוימת בתור סכום או טור של פונקציות פשוטות יותר. בצורה זו ניתן להעמיק את ההבנה של התנהגות הפונקציה על ידי הבנת התנהגות אברי הסכום (הטור). טור פורייה הוא סוג של טור שכזה, שבו מוצגת פונקציה כסכום (טור) של פונקציות מחזוריות.

בפיזיקה ובהנדסה, בעיקר בתחומים הנוגעים לגלים, נוח להציג את המידע בצורת סכום (טור) של הרמוניות. גם יישומי מחשב העוסקים בעיבוד תמונה וקול משתמשים רבות בטורי פורייה לצורך ניתוח ודחיסה של המידע.

בניסוח פורמלי יותר, טור פורייה הוא הצגה של פונקציה שריבועה הוא אינטגרבילי-לבג בקטע סופי כטור אינסופי של פונקציות הרמוניות וטריגונומטריות. זוהי בעצם גרסה בדידה להתמרת פורייה (או טרנספורם פורייה).

מבוא ורקע כללי

טור פורייה הוא תוצאה פרטית של התורה העוסקת בבסיסים אורתונורמליים על מרחב הילברט.

מבחינה אלגברית, מדובר בהצגת איבר במרחב וקטורי על ידי צירוף ליניארי של איברי בסיס אורתונורמלי של המרחב. כלומר, עבור בסיס אורתונורמלי $\left\{{\hat {e}}\right\}$ האיבר ${\vec {x}}$ מוצג על ידי:

{\vec {x}}=\sum _{\alpha \in \Lambda }{a_{\alpha }{\hat {e_{\alpha }}}}

מכיוון שהבסיס הוא אורתונורמלי, את המקדמים אפשר לחשב באמצעות הטלה:

a_{n}=\langle {\vec {x}},{\hat {e_{n}}}\rangle

ומובטח שהמקדמים יתאפסו עבור כל איברי הבסיס פרט לקבוצה בת-מנייה. לכן ניתן לכתוב את ההצגה של כל איבר במרחב זה בצורה זו:

{\vec {x}}=\sum _{n=1}^{\infty }{\langle {\vec {x}},{\hat {e_{n}}}\rangle {\hat {e_{n}}}}

טור פורייה הוא מקרה פרטי של בנייה זו. מאחר שמדובר בטור אינסופי, יש לטפל בבעיות התכנסות ולהראות שהטור אכן מתכנס אל האיבר שאותו מציגים. בסעיפים הבאים נעסוק בנושאים הקשורים ישירות לטור פורייה הטריגונומטרי. זהו טור פורייה הנפוץ ביותר ולעיתים קרובות כאשר אומרים "טור פורייה" סתם, מתכוונים אליו.

הגדרה פורמלית

תהי $f$ פונקציה, $f\in L^{2}[-\pi ,\pi ]$ , כאשר $L^{2}[-\pi ,\pi ]$ הוא אוסף הפונקציות המדידות שריבוען אינטגרבילי-לבג בקטע. אזי אפשר להציג את $f$ כפיתוח לטור אינסופי באופן הבא:

f(x)=\sum _{n=-\infty }^{\infty }F_{n}\,e^{inx}

כאשר מקדמי פורייה, $F_{n}$ , נתונים על ידי:

F_{n}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)\,e^{-inx}\,dx

(נוסחה זאת נובעת משיקולי אורתוגונליות. ראו להלן). כל איבר בטור זה נקרא אופן תנודה, Fourier mode או הרמוניה.

על ידי שימוש בנוסחת אוילר $e^{inx}=\cos(nx)+i\sin(nx)\,\!$ אפשר להציג את טור פורייה כצירוף ליניארי של סינוסים וקוסינוסים באופן הבא:

f(x)={\frac {1}{2}}a_{0}+\sum _{n=1}^{\infty }\left[a_{n}\cos(nx)+b_{n}\sin(nx)\right]

כאשר המקדמים נתונים על ידי:

a_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\cos(nx)\,dx

b_{n}={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\sin(nx)\,dx

את הקשר בין מקדמים אלה למקדמים $F_{n}$ ניתן לחלץ בקלות והוא $F_{n}=(a_{n}-ib_{n})/2\,\!$ כאשר $F_{n}=F_{-n}^{*}$ . באמצעות החלפת משתנים ניתן להכליל את הפיתוח הזה לכל קטע סופי שהוא.

דוגמה

תהי $f$ הפונקציה הליניארית $f(x)={\frac {x}{\pi }}$ בקטע $[-\pi ,\pi ]$ . כדי שטור פורייה שלה יהיה תקף גם מחוץ לקטע זה, נצטרך להרחיב אותה באופן מחזורי. הפונקציה המורחבת נקראת גם "גל שן מסור". הרחבה זו איננה פונקציה רציפה, אך הפיתוח לטור פורייה עדיין קיים.

גרף של פונקציית גל שן-מסור

ניתן לחשב את מקדמי פוריה שלה בהצגה הטריגונומטרית (נוח להשתמש בהצגה זו עבור פונקציות זוגיות או אי-זוגיות כפי שנראה להלן).

מאחר ש־ $f(x)$ היא פונקציה אי-זוגית, ו־ $\cos(nx)$ הן פונקציות זוגיות לכל $n$ , המכפלות הן פונקציות אי זוגיות. כתוצאה מכך כל המקדמים של הקוסינוסים מתאפסים:

{\begin{aligned}a_{0}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)dx={\frac {1}{\pi }}\int _{-\pi }^{\pi }{\frac {x}{\pi }}dx=0\\a_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\cos(nx)dx={\frac {1}{\pi }}\int _{-\pi }^{\pi }{\frac {x}{\pi }}\cos(nx)dx=0\end{aligned}}

כעת, ניתן לחשב את מקדמי הסינוסים:

{\begin{aligned}b_{n}&={\frac {1}{\pi }}\int _{-\pi }^{\pi }f(x)\sin(nx)dx={\frac {1}{\pi }}\int _{-\pi }^{\pi }{\frac {x}{\pi }}\sin(nx)dx\\&={\frac {2}{\pi }}\int _{0}^{\pi }{\frac {x\sin(nx)}{\pi }}dx={\frac {2}{\pi }}\left(\left[-{\frac {x\cos(nx)}{n\pi }}\right]_{0}^{\pi }+\left[{\frac {\sin(nx)}{n^{2}\pi }}\right]_{0}^{\pi }\right)\\&={\frac {2}{\pi }}{\frac {(-1)^{n+1}}{n}}\end{aligned}}

בסך הכל, טור פורייה של $f(x)={\frac {x}{\pi }}$ בקטע הוא:

{\begin{aligned}f(x)&={\frac {x}{\pi }}={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }(a_{n}\cos(nx)+b_{n}\sin(nx))\\&={\frac {2}{\pi }}\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}\sin(nx),\quad \forall x\in (-\pi ,\pi )\end{aligned}}

חישוב סכומים חלקיים של איברי הטור ייתן קירוב של הפונקציה, שיהיה טוב יותר ככל שניקח יותר איברים, כמודגם בתמונה.

גרף המכיל סדרת קירובים לפונקציית גל שן-משור באמצעות סכומים חלקיים של טור פורייה.

בטור זה אפשר להשתמש כדי לחשב את הערך של פונקציית זטא של רימן עבור $s=2$ בעזרת שוויון פרסבל המאפשר להמיר את בעיית חישוב הטור לבעיה של חישוב אינטגרלים (אותה אפשר לחשב מפורשות).

תאוריה

המרחב L²

המרחב $L^{2}[-\pi ,\pi ]$ כולל את הפונקציות שריבוען אינטגרבילי-לבג בקטע, כלומר, עבור $f\in L^{2}[-\pi ,\pi ]$ , ‏ $f$ פונקציה מדידה ומתקיים $\int _{-\pi }^{\pi }{|f(t)|^{2}dt}<\infty$ . מרחב זה הוא מרחב הילברט עם המכפלה הפנימית $\langle f,g\rangle =\int _{-\pi }^{\pi }{f(t){\bar {g}}(t)dt}$ , כאשר ${\bar {g}}(t)$ הוא הצמוד המרוכב של $g(t)$ .

במרחב הילברט זה – על אף שהוא מממד אינסופי – קיימת מערכת אורתונורמלית שלמה, הפורשת קבוצה צפופה במרחב. ניתן לראות בכך הכללה של מושג הבסיס (ובפרט בסיס אורתונורמלי) של מרחב וקטורי מממד סופי (לעיתים קוראים גם למערכת אורתונורמלית שלמה אינסופית בשם "בסיס"). המתמטיקאי ז'וזף פורייה וממשיכיו הוכיחו שהפונקציות ההרמוניות יוצרות מערכת אורתונורמלית שלמה.

טור פורייה הוא למעשה דרך להציג איבר במרחב $L^{2}$ כצירוף ליניארי (בדרך כלל אינסופי) של איברי הבסיס הזה, כאשר המקדמים של הצירוף הליניארי נקראים מקדמי פורייה. ניתן לעשות זאת גם עם בסיסים אורתונורמליים אחרים, אבל ביישומים רבים מתגלה השימוש בטורי פורייה כיעיל במיוחד.

אורתונורמליות

בסיס ההרמוניות $\left\{{\frac {e^{inx}}{\sqrt {2\pi }}}\right\}_{n\in \mathbb {Z} }$ הוא בסיס אורתונורמלי, כי:

\langle {\frac {e^{inx}}{\sqrt {2\pi }}},{\frac {e^{imx}}{\sqrt {2\pi }}}\rangle ={\frac {1}{2\pi }}\int _{-\pi }^{\pi }e^{inx}e^{-imx}\,dx=\delta _{n,m}

כאשר $\delta _{n,m}$ היא הדלתא של קרונקר.

מכאן נובעות הנוסחאות לחישוב המקדמים:

{\frac {1}{2\pi }}\int _{-\pi }^{\pi }{f(t)e^{-int}dt}={\frac {1}{2\pi }}\langle f(t),e^{int}\rangle ={\frac {1}{2\pi }}\langle \sum _{k=-\infty }^{\infty }{F_{k}e^{ikt}},e^{int}\rangle =\sum _{k=-\infty }^{\infty }{F_{k}{\frac {1}{2\pi }}\langle e^{ikt},e^{int}\rangle }=\sum _{k=-\infty }^{\infty }{F_{k}\delta _{n,k}}=F_{n}

באופן דומה גם בסיס הסינוסים והקוסינוסים הוא אורתונורמלי:

{\frac {1}{\pi }}\int _{-\pi }^{\pi }{\cos(nt)\cos(mt)\ dt}=\delta _{m,n}

{\frac {1}{\pi }}\int _{-\pi }^{\pi }{\sin(nt)\cos(mt)\ dt}=0\ \ \ \

{\frac {1}{\pi }}\int _{-\pi }^{\pi }{\sin(nt)\sin(mt)\ dt}=\delta _{m,n}

אפשר להשתכנע בכך בבדיקה ישירה או מכך שמקבלים אותו על ידי התמרה אוניטרית מבסיס ההרמוניות.

התכנסות

כאשר עוסקים בהתכנסות של טור פורייה יש להבדיל בין התכנסות בנורמה של הטור, לבין התכנסות נקודתית.

ההתכנסות בנורמה פירושה שהטור מתכנס במרחב $L^{2}$ על פי הנורמה המוגדרת בו. כלומר, מתקיים:

\lim _{N\rightarrow \infty }\int _{-\pi }^{\pi }\left|f(x)-\sum _{n=-N}^{N}F_{n}\,e^{inx}\right|^{2}\,dx=0

במילים פשוטות: כאשר מגדילים את מספר האיברים בטור החלקי של $f$ לאינסוף, הנורמה של ההפרש בין הפיתוח החלקי לבין $f$ (שהיא האינטגרל של פונקציית ריבוע ההפרש) שואפת לאפס. תכונה זו מתקיימת עבור כל טור פורייה, בהיותו הצגת איבר ב- $L^{2}$ על פי בסיס אורתונורמלי.

התכנסות בנורמה לא מחייבת התכנסות של הטור לערך של $f$ בכל נקודה בקטע – ההתכנסות הנקודתית של טור פורייה היא תכונה מורכבת יותר, ומחקר רב עוסק במציאת תנאים שבהם היא תתקיים במסגרת האנליזה ההרמונית.

בחישוב של טור פורייה לפונקציה נתונה $f$ יש שני שלבים הפוכים זה לזה. בשלב ראשון מחשבים, מכיוון שעבור פונקציה מחזורית קיים שוויון מהצורה $f(x)=\sum _{n}(a_{n}\sin(nx)+b_{n}\cos(nx))$ , את המקדמים המספריים $a_{n}$ ו־ $b_{n}$ . חישוב כזה ניתן לערוך לכל פונקציה השייכת למרחב הפונקציות $L^{2}$ . לאחר מכן, עבור הצגת הפונקציה באמצעות המקדמים שהתקבלו, נדרש שהטור באגף ימין יתכנס לערכה של הפונקציה בנקודה $x$ לכל $x$ .

כאשר פיתח פורייה את התאוריה שלו, ב-1807, לא היו בידיו כלים שיענו על הצורך בהתכנסות נקודתית, וזו הסיבה העיקרית לכך שעבודתו נדחתה בתחילה על ידי מתמטיקאים חשובים בני זמנו. בשאלה איזה הנחות של רציפות נכללות בהגדרת מושג הפונקציה היה ערפול מסוים במחצית הראשונה של המאה ה-19, ועבודתו של פורייה רק הקשתה על הבהרת התמונה. ב־1913 ניסח האנליטיקאי הרוסי ניקולאי לוזין את ההשערה שטור פורייה של פונקציה רציפה יתכנס נקודתית בכל מקום, אלא שב־1926 מצא מתמטיקאי רוסי אחר, אנדריי קולמוגורוב, דוגמה נגדית שהפריכה השערה זו.

פתרון לבעיה זו ניתן על-ידי המתמטיקאי השוודי לנרט קרלסון ב-1966, כאשר הוא הוכיח שלכל פונקציה ששייכת למרחב $L^{2}$ , ובפרט לכל פונקציה רציפה, יש טור פורייה המתכנס אליה כמעט בכל נקודה בקטע (מידתה של קבוצת הנקודות שבה אין התכנסות היא אפס). כלומר ההתכנסות של טור פורייה במקרים כאלה היא כמעט בכל מקום. על עבודתו זו, שנחשבה לפריצת דרך באנליזה הרמונית, ועל עבודות רבות אחרות, זכה קרלסון בפרס אבל לשנת 2006.

תופעת גיבס

תופעת גיבס היא תופעה שבה טור פורייה של פונקציה שאינה רציפה בנקודה, מתכנס בנקודה זו לממוצע הגבולות מימין ומשמאל ( $(f(x_{-})+f(x_{+}))/2$ ). יתרה מכך, סביב נקודת אי-רציפות מתקבלות תנודות חזקות; ככל שמוסיפים יותר איברים לקירוב, מצטמצמת הסביבה בה מופיעות התנודות, אך גובהן לא נחלש.

דעיכת מקדמי פורייה

קיים קשר ישיר בין "מידת החלקות" של פונקציה מסוימת לקצב הדעיכה של מקדמי פורייה שלה, קשר שבתורו מכתיב את טיב הקירוב של הפונקציה על ידי סכום פורייה סופי. עבור פונקציה ממחלקה $C^{k}$ , כלומר הגזירה ברציפות $k$ פעמים, הערכים המוחלטים של מקדמי פורייה שלה אינם דועכים מהר יותר מ- ${\frac {1}{n^{k+2+\epsilon }}}$ לכל $\epsilon >0$ . תופעה זו נובעת מן העובדות הבאות:

עבור פונקציות רציפות למקוטעין: "אבני הבניין" של טורי פורייה הן הרמוניות טריגונומטריות, שהן עצמן פונקציות רציפות במידה שווה. כיוון שכך, ניתן להראות שבסביבת נקודת אי-רציפות מסוג ראשון סדרת הסכומים החלקיים של טור פורייה לא יכולה להתכנס במידה שווה לממוצע של הגבול הימני והשמאלי של הפונקציה (תמיד ישנו "רעש" סופי מסוים בסביבת נקודת האי רציפות; ראו גם: תופעת גיבס). על פי מבחן M של ויירשטראס, התנהגות זו חייבת לבוא לידי ביטוי בהתכנסות בתנאי של סדרת המקדמים (ולא בהתכנסות בהחלט). מצד שני, לפי למת רימן-לבג, מקדמי פורייה שואפים בערכם המוחלט לאפס כאשר $n$ שואף לאינסוף. לכן, ממבחן ההשוואה הגבולי עם הטור ההרמוני המתבדר, נובע שהערכים המוחלטים של מקדמי פורייה דועכים לאפס לאט יותר מאשר ${\frac {1}{n^{1+\epsilon }}}$ , לכל $\epsilon >0$ .
עבור פונקציה ממחלקה $C^{k}$ , ניתן להסתכל על הנגזרת ה- $k+1$ , שהיא על פי ההנחה פונקציה רציפה למקוטעין, ואז לבצע אינטגרציה לאחור $k+1$ פעמים כדי לשחזר את הפונקציה המקורית. בכל צעד אינטגרציה, מקדם פורייה ה- $n$ מוכפל ב- ${\frac {1}{n}}$ , ולכן מקדם פורייה ה- $n$ של $f(x)$ מתנהג כמו $a_{n}\propto {\frac {1}{n^{k+2}}}$ . בפרט, נובע מכך שעבור פונקציות חלקות (ממחלקה $C^{\infty }$ ), מקדמי פורייה דועכים "מהר מאוד" לאפס.

תכונות

בסעיף זה יסומנו הפונקציות:

f(x)=\sum _{n=-\infty }^{\infty }{F_{n}e^{inx}}\;;\quad g(x)=\sum _{n=-\infty }^{\infty }{G_{n}e^{inx}}\;;\quad h(x)=\sum _{n=-\infty }^{\infty }{H_{n}e^{inx}}

כאשר מונח ש- $f$ ,‏ $g$ ו־ $h$ הן פונקציות המוגדרות על כל הישר באמצעות המשכה מחזורית של הגדרתן בקטע $[-\pi ,\pi ]$ .

ליניאריות

אם $h(x)=\alpha f(x)+\beta g(x)$ , אזי $H_{n}=\alpha F_{n}+\beta G_{n}$ .

זהויות פלנשרל ופרסבל

הזהויות הבאות מראות את האוניטריות של הפירוק לטור פורייה. כלומר, פעולה זו שומרת על נורמה ומכפלה פנימית.

זהות פלנשרל (Plancherel identity):

\sum _{n=-\infty }^{\infty }F_{n}G_{n}^{*}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)g^{*}(x)\,dx

זהות פרסבל (על שם מארק אנטואן פרסבל):

\sum _{n=-\infty }^{\infty }|F_{n}|^{2}={\frac {1}{2\pi }}\int _{-\pi }^{\pi }|f(x)|^{2}dx\,

ובבסיס הטריגונומטרי הממשי

{\frac {a_{0}^{2}}{4}}+{\frac {1}{2}}\sum _{n=1}^{\infty }\left(a_{n}^{2}+b_{n}^{2}\right)={\frac {1}{2\pi }}\int _{-\pi }^{\pi }f(x)^{2}dx

משפטים אלה אפשר להוכיח באמצעות אורתוגונליות.

תכונת ההזזה

אם $g(x)=f(x-y)\,\!$ , אזי $G_{n}=e^{-iny}F_{n}\,\!$

תכונת הקונבולוציה

אם $h$ היא קונבולוציה ציקלית של $f$ ו- $g$ , כלומר:

h(t)=\int _{-\pi }^{\pi }f(t')g(t-t')\,dt'

כאשר $g$ היא מחזורית עם מחזור $2\pi$ , אזי טור פורייה של $h$ מקיים:

H_{n}=2\pi \,F_{n}G_{n}\,

באופן הפוך, אם המקדמים $H_{n}$ הם קונבולוציה של $F_{n}$ ו־ $G_{n}$ , כלומר:

H_{k}=\sum _{n=-\infty }^{\infty }F_{n}G_{k-n}

אזי בהכרח:

h(t)=f(t)g(t)\,

תכונות אלה מוכחות באמצעות אורתוגונליות.

טורי פורייה בקטע כלשהו

נניח שנתונה פונקציה $g:[a,a+\tau ]\to \mathbb {R}$ , אינטגרבילית בריבוע בקטע זה, וממשיכים אותה באופן מחזורי בכל הישר הממשי, אזי טור פורייה שלה מוגדר על ידי: