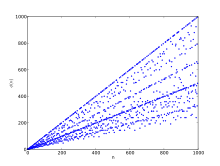
פונקציית אוילר (על שם המתמטיקאי השווייצרי לאונרד אוילר ) היא דוגמה חשובה לפונקציה אריתמטית .
1000 הערכים הראשונים של פונקציית אוילר מקובל לסמנה באות היוונית
ϕ
{\displaystyle \phi }
פי ), והיא מוגדרת באופן הבא:
ϕ
(
n
)
{\displaystyle \phi (n)}
המספרים הטבעיים הקטנים מ-
n
{\displaystyle n}
זרים לו.
ϕ
(
5
)
=
|
{
1
,
2
,
3
,
4
}
|
=
4
,
ϕ
(
6
)
=
|
{
1
,
5
}
|
=
2
{\displaystyle \phi (5)=|\{1,2,3,4\}|=4,\phi (6)=|\{1,5\}|=2}
ϕ
(
1
)
=
|
{
1
}
|
=
1
{\displaystyle \phi (1)=|\{1\}|=1}
חבורת אוילר
U
n
{\displaystyle U_{n}}
n
{\displaystyle n}
הפונקציה מוכרת ושימושית בעיקר בזכות משפט אוילר , שלפיו הסדר של כל איבר בחבורת אוילר מסדר
n
{\displaystyle n}
מחלק את
ϕ
(
n
)
{\displaystyle \phi (n)}
אם
p
{\displaystyle p}
מספר ראשוני , אזי כל המספרים הקטנים מ-
p
{\displaystyle p}
זרים לו, ולכן
ϕ
(
p
)
=
p
−
1
{\displaystyle \phi (p)=p-1}
p
s
{\displaystyle p^{s}}
p
{\displaystyle p}
p
s
−
1
{\displaystyle p^{s-1}}
ϕ
(
p
s
)
=
p
s
−
p
s
−
1
=
p
s
−
1
(
p
−
1
)
=
p
s
(
1
−
1
p
)
{\displaystyle \phi (p^{s})=p^{s}-p^{s-1}=p^{s-1}(p-1)=p^{s}\left(1-{\frac {1}{p}}\right)}
משפט השאריות הסיני נובע שפונקציית אוילר כפלית , כלומר
ϕ
(
n
1
n
2
)
=
ϕ
(
n
1
)
ϕ
(
n
2
)
{\displaystyle \phi (n_{1}n_{2})=\phi (n_{1})\phi (n_{2})}
n
1
,
n
2
{\displaystyle n_{1},n_{2}}
ϕ
(
n
)
=
n
(
1
−
1
p
1
)
⋯
(
1
−
1
p
k
)
{\displaystyle \phi (n)=n\left(1-{\frac {1}{p_{1}}}\right)\cdots \left(1-{\frac {1}{p_{k}}}\right)}
כאשר
p
1
,
…
,
p
k
{\displaystyle p_{1},\ldots ,p_{k}}
n
{\displaystyle n}
ϕ
(
45
)
=
45
(
1
−
1
3
)
(
1
−
1
5
)
=
24
{\displaystyle \phi (45)=45\left(1-{\frac {1}{3}}\right)\left(1-{\frac {1}{5}}\right)=24}
n
=
p
1
k
1
⋯
p
r
k
r
{\displaystyle n=p_{1}^{k_{1}}\cdots p_{r}^{k_{r}}}
ϕ
(
n
)
=
ϕ
(
p
1
k
1
)
⋯
ϕ
(
p
r
k
r
)
=
p
1
k
1
(
1
−
1
p
1
)
⋯
p
r
k
r
(
1
−
1
p
r
)
=
p
1
k
1
⋯
p
r
k
r
(
1
−
1
p
1
)
⋯
(
1
−
1
p
r
)
=
n
(
1
−
1
p
1
)
⋯
(
1
−
1
p
r
)
{\displaystyle {\begin{aligned}\phi (n)&=\phi (p_{1}^{k_{1}})\cdots \phi (p_{r}^{k_{r}})\\&=p_{1}^{k_{1}}\left(1-{\frac {1}{p_{1}}}\right)\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{r}}}\right)\\&=p_{1}^{k_{1}}\cdots p_{r}^{k_{r}}\left(1-{\frac {1}{p_{1}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\\&=n\left(1-{\frac {1}{p_{1}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\end{aligned}}}
פונקציית אוילר מקיימת את הזהות
∑
d
|
n
ϕ
(
d
)
=
n
{\displaystyle \sum _{d|n}\phi (d)=n}
סדרים של איברים בחבורה הציקלית
Z
/
n
Z
{\displaystyle \mathbb {Z} /n\mathbb {Z} }
נוכל להסתכל על הזהות הזו כקונבולוציה
φ
∗
1
=
id
{\displaystyle \varphi *1={\text{id}}}
id
{\displaystyle {\text{id}}}
פונקציית הזהות . לכן, מנוסחת ההיפוך של מביוס נובע כי
φ
(
n
)
=
(
μ
∗
id
)
(
n
)
=
∑
d
|
n
μ
(
d
)
n
d
=
n
∑
d
|
n
μ
(
d
)
d
{\displaystyle \varphi (n)=(\mu *{\text{id}})(n)=\sum _{d|n}\mu (d){\frac {n}{d}}=n\sum _{d|n}{\frac {\mu (d)}{d}}}
כאשר
μ
{\displaystyle \mu }
פונקציית מביוס .
נוכל לתת הוכחה נוספת, המבוססת על הנוסחה
ϕ
(
n
)
=
n
∏
p
|
n
(
1
−
1
p
)
{\displaystyle \phi (n)=n\prod _{p|n}\left(1-{\frac {1}{p}}\right)}
p
1
,
…
,
p
r
{\displaystyle p_{1},\ldots ,p_{r}}
n
{\displaystyle n}
∏
p
|
n
(
1
−
1
p
)
=
(
1
−
1
p
1
)
⋯
(
1
−
1
p
r
)
=
∑
k
=
0
r
∑
1
≤
i
1
<
⋯
<
i
k
≤
r
(
−
1
)
k
p
i
1
⋯
p
i
k
=
∑
k
=
0
r
∑
1
≤
i
1
<
⋯
<
i
k
≤
r
μ
(
p
i
1
⋯
p
i
k
)
p
i
1
⋯
p
i
k
=
∑
d
|
n
μ
(
d
)
d
{\displaystyle {\begin{aligned}\prod _{p|n}\left(1-{\frac {1}{p}}\right)&=\left(1-{\frac {1}{p_{1}}}\right)\cdots \left(1-{\frac {1}{p_{r}}}\right)\\&=\sum _{k\,=\,0}^{r}\sum _{1\leq i_{1}<\cdots <i_{k}\leq r}{\frac {(-1)^{k}}{p_{i_{1}}\cdots p_{i_{k}}}}\\&=\sum _{k\,=\,0}^{r}\sum _{1\leq i_{1}<\cdots <i_{k}\leq r}{\frac {\mu (p_{i_{1}}\cdots p_{i_{k}})}{p_{i_{1}}\cdots p_{i_{k}}}}\\&=\sum _{d|n}{\frac {\mu (d)}{d}}\end{aligned}}}
שהרי לכל מחלק
d
>
1
,
d
|
n
{\displaystyle d>1,d|n}
μ
(
d
)
=
0
{\displaystyle \mu (d)=0}
לכל
n
>
2
{\displaystyle n>2}
ϕ
(
n
)
{\displaystyle \phi (n)}
מספר זוגי . ניתן לראות זאת מתכונת הכפליות. אם
n
=
2
k
{\displaystyle n=2^{k}}
k
>
1
{\displaystyle k>1}
ϕ
(
n
)
=
2
k
(
1
−
0.5
)
=
2
k
−
1
{\displaystyle \phi (n)=2^{k}(1-0.5)=2^{k-1}}
n
{\displaystyle n}
p
{\displaystyle p}
n
=
p
k
m
{\displaystyle n=p^{k}m}
ϕ
(
n
)
=
ϕ
(
p
k
)
ϕ
(
m
)
=
p
k
−
1
(
p
−
1
)
ϕ
(
m
)
{\displaystyle \phi (n)=\phi (p^{k})\phi (m)=p^{k-1}(p-1)\phi (m)}
p
−
1
{\displaystyle p-1}
הערך הממוצע של הפונקציה הוא[ 1]
ϕ
(
1
)
+
⋯
+
ϕ
(
n
)
n
∼
3
π
2
n
{\displaystyle {\frac {\phi (1)+\cdots +\phi (n)}{n}}\sim {\frac {3}{\pi ^{2}}}n}
ϕ
(
n
)
n
/
ln
(
ln
(
n
)
)
{\displaystyle {\frac {\phi (n)}{n/\ln(\ln(n))}}}
e
−
γ
{\displaystyle e^{-\gamma }}
γ
{\displaystyle \gamma }
קבוע אוילר-מסקרוני .
ניתן לכתוב את טור דיריכלה של פונקציית אוילר באופן הבא:
F
ϕ
(
s
)
=
∑
n
=
1
∞
ϕ
(
n
)
n
s
=
ζ
(
s
−
1
)
ζ
(
s
)
{\displaystyle F_{\phi }(s)=\sum _{n\,=\,1}^{\infty }{\frac {\phi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}}
כאשר
ζ
{\displaystyle \zeta }
פונקציית זטא של רימן .
Hardy and Wright, An Introduction to the Theory of Numbers, פרק 18.
^ זו השערה לא מפורסמת של גאוס מ-1796. פורסמה לראשונה על ידי דיריכלה ב-1849, והוכחה לבסוף על ידי Arnold Walfisz.