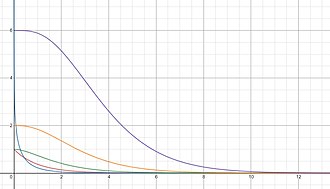
פונקציית גמא הלא שלמה מוגדרת על ידי אינטגרל בעל אותו אינטגרנד כמו פונקציית גמא , אך עם גבולות אינטגרציה שונים:
פונקציית הגמא העליונה הלא שלמה, עבור מספר ערכים שלמים של s: 0 (כחול), 1 (אדום), 2 (ירוק), 3 (כתום), 4 (סגול). ישנם שני סוגים של פונקציית גמא הלא שלמה: עליונה ותחתונה.
פונקציית גמא הלא שלמה העליונה מוגדרת:
Γ
(
s
,
x
)
=
∫
x
∞
t
s
−
1
e
−
t
d
t
.
{\displaystyle \Gamma (s,x)=\int _{x}^{\infty }t^{s-1}\,e^{-t}\,{\rm {d}}t.\,\!}
פונקציית גמא הלא שלמה התחתונה מוגדרת:
γ
(
s
,
x
)
=
∫
0
x
t
s
−
1
e
−
t
d
t
.
{\displaystyle \gamma (s,x)=\int _{0}^{x}t^{s-1}\,e^{-t}\,{\rm {d}}t.\,\!}
עריכה
מההגדרה אפשר להבין כי:
γ
(
s
,
x
)
+
Γ
(
s
,
x
)
=
Γ
(
s
)
{\displaystyle \gamma (s,x)+\Gamma (s,x)=\Gamma (s)\!}
על ידי אינטגרציה בחלקים אפשר להגיע למסקנה:
Γ
(
s
,
x
)
=
(
s
−
1
)
Γ
(
s
−
1
,
x
)
+
x
s
−
1
e
−
x
{\displaystyle \Gamma (s,x)=(s-1)\Gamma (s-1,x)+x^{s-1}e^{-x}\!}
γ
(
s
,
x
)
=
(
s
−
1
)
γ
(
s
−
1
,
x
)
−
x
s
−
1
e
−
x
{\displaystyle \gamma (s,x)=(s-1)\gamma (s-1,x)-x^{s-1}e^{-x}\!}
Γ
(
s
,
x
)
=
(
s
−
1
)
!
e
−
x
∑
k
=
0
s
−
1
x
k
k
!
{\displaystyle \Gamma (s,x)=(s-1)!\,e^{-x}\sum _{k=0}^{s-1}{\frac {x^{k}}{k!}}}
Γ
(
s
,
0
)
=
Γ
(
s
)
{\displaystyle \Gamma (s,0)=\Gamma (s)\!}
Γ
(
1
,
x
)
=
e
−
x
{\displaystyle \Gamma (1,x)=e^{-x}\!}
γ
(
1
,
x
)
=
1
−
e
−
x
{\displaystyle \gamma (1,x)=1-e^{-x}\!}
עריכה
∂
Γ
(
s
,
x
)
∂
x
=
−
x
s
−
1
e
x
{\displaystyle {\frac {\partial \Gamma (s,x)}{\partial x}}=-{\frac {x^{s-1}}{e^{x}}}}
הגדרת מקרה מיוחד של פונקציית "G" של ("Meijer G") מאייר[ 1]
T
(
m
,
s
,
x
)
=
G
m
−
1
,
m
m
,
0
(
0
,
0
,
…
,
0
s
−
1
,
−
1
,
…
,
−
1
|
x
)
{\displaystyle T(m,s,x)=G_{m-1,\,m}^{\,m,\,0}\!\left(\left.{\begin{matrix}0,0,\dots ,0\\s-1,-1,\dots ,-1\end{matrix}}\;\right|\,x\right)}
T
(
m
,
s
,
z
)
=
−
(
−
1
)
m
−
1
(
m
−
2
)
!
d
m
−
2
d
t
m
−
2
[
Γ
(
s
−
t
)
z
t
−
1
]
|
t
=
0
+
∑
n
=
0
∞
(
−
1
)
n
z
s
−
1
+
n
n
!
(
−
s
−
n
)
m
−
1
{\displaystyle T(m,s,z)=-{\frac {(-1)^{m-1}}{(m-2)!}}{\frac {{\rm {d}}^{m-2}}{{\rm {d}}t^{m-2}}}\left[\Gamma (s-t)z^{t-1}\right]{\Big |}_{t=0}+\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{s-1+n}}{n!(-s-n)^{m-1}}}}
|
z
|
<
1
{\displaystyle |z|<1}
∂
Γ
(
s
,
x
)
∂
s
=
ln
x
Γ
(
s
,
x
)
+
x
T
(
3
,
s
,
x
)
{\displaystyle {\frac {\partial \Gamma (s,x)}{\partial s}}=\ln x\Gamma (s,x)+x\,T(3,s,x)}
∂
2
Γ
(
s
,
x
)
∂
s
2
=
ln
2
x
Γ
(
s
,
x
)
+
2
x
[
ln
x
T
(
3
,
s
,
x
)
+
T
(
4
,
s
,
x
)
]
{\displaystyle {\frac {\partial ^{2}\Gamma (s,x)}{\partial s^{2}}}=\ln ^{2}x\Gamma (s,x)+2x[\ln x\,T(3,s,x)+T(4,s,x)]}
∂
m
Γ
(
s
,
x
)
∂
s
m
=
ln
m
x
Γ
(
s
,
x
)
+
m
x
∑
n
=
0
m
−
1
P
n
m
−
1
ln
m
−
n
−
1
x
T
(
3
+
n
,
s
,
x
)
{\displaystyle {\frac {\partial ^{m}\Gamma (s,x)}{\partial s^{m}}}=\ln ^{m}x\Gamma (s,x)+mx\,\sum _{n=0}^{m-1}P_{n}^{m-1}\ln ^{m-n-1}x\,T(3+n,s,x)}
P
j
n
=
(
n
j
)
j
!
=
n
!
(
n
−
j
)
!
.
{\displaystyle P_{j}^{n}=\left({\begin{array}{l}n\\j\end{array}}\right)j!={\frac {n!}{(n-j)!}}.}
γ
(
s
,
x
)
x
s
→
1
s
{\displaystyle {\frac {\gamma (s,x)}{x^{s}}}\rightarrow {\frac {1}{s}}}
x
→
0
{\displaystyle x\rightarrow 0}
Γ
(
s
,
x
)
x
s
→
−
1
s
{\displaystyle {\frac {\Gamma (s,x)}{x^{s}}}\rightarrow -{\frac {1}{s}}}
x
→
0
{\displaystyle x\rightarrow 0}
ℜ
(
s
)
<
0
{\displaystyle \Re (s)<0\,}
γ
(
s
,
x
)
→
Γ
(
s
)
{\displaystyle \gamma (s,x)\rightarrow \Gamma (s)}
x
→
∞
{\displaystyle x\rightarrow \infty }
Γ
(
s
,
x
)
x
s
−
1
e
−
x
→
1
{\displaystyle {\frac {\Gamma (s,x)}{x^{s-1}e^{-x}}}\rightarrow 1}
x
→
∞
{\displaystyle x\rightarrow \infty }
^ K.O. Geddes, M.L. Glasser, R.A. Moore and T.C. Scott, Evaluation of Classes of Definite Integrals Involving Elementary Functions via Differentiation of Special Functions , AAECC (Applicable Algebra in Engineering, Communication and Computing), vol. 1, (1990), pp. 149-165, [1]
![{\displaystyle T(m,s,z)=-{\frac {(-1)^{m-1}}{(m-2)!}}{\frac {{\rm {d}}^{m-2}}{{\rm {d}}t^{m-2}}}\left[\Gamma (s-t)z^{t-1}\right]{\Big |}_{t=0}+\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{s-1+n}}{n!(-s-n)^{m-1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e9d7c30bc1fcd8805304d0556ca97cef8b4e049)
![{\displaystyle {\frac {\partial ^{2}\Gamma (s,x)}{\partial s^{2}}}=\ln ^{2}x\Gamma (s,x)+2x[\ln x\,T(3,s,x)+T(4,s,x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a60a14278607f4979d30c0a2a23585b1413cda3)
