פורטל:מתמטיקה/אנימציה נבחרת/גלריה

אנימציה נבחרת

1

סרטון של זום לתוך קבוצת מנדלברוט

סרטון של זום לתוך קבוצת מנדלברוט, קבוצה של מספרים מרוכבים אשר הגבול של ייצוגן הגאומטרי מהווה את אחת הדוגמאות המוכרות ביותר של פרקטלים במתמטיקה.

2

מסלולה של נקודה על שפתו של מעגל המתגלגל על שפתו מעגל אחר בעל רדיוס גדול פי ארבעה נקראת "אסטרואידה". משוואתה של אסטרואידה היא $x^{2/3}+y^{2/3}=1\,$.

3

אנימציה תלת-ממדית המציגה את היטליו של טסרקט, גוף ארבע ממדי המהווה הכללה של הקובייה התלת־ממדית.

4

איור הממחיש את מושג האינטגרל הקווי.

5

ציקלואידה

עקומה שמתארת את מסלולה של נקודה קבועה על גבי מעגל המתגלגל ללא החלקה על גבי קו ישר. זה המסלול שפותר את בעיית הברכיסטוכרון, בעיית "הזמן הקצר ביותר".

6

כיסוי האוריינטציות של טבעת מביוס.

כיסוי האוריינטציות הוא כלי לחקר יריעות לא אוריינטביליות. עבור משטח במרחב, ניתן לתאר את כיסוי האוריינטציות באופן הבא: נדמיין שהמשטח עשוי מנייר דו-שכבתי. נפריד את השכבות. היריעה שתתקבל תהיה מרחב הכיסוי של כיסוי האוריינטציות. העתקת הכיסוי תהיה ההדבקה של שתי השכבות בחזרה.

במקרה של טבעת מביוס (זאת אומרת טבעת עם חצי פיתול) היריעה המתקבלת לאחר הפרדת השכבות היא טבעת עם פיתול שלם. יריעה זאת דיפאומורפית לטבעת רגילה, ובפרט אוריינטבילית.

7

בנייה של פתית השלג של קוך, פרקטל שתואר לראשונה על ידי הלגה פון קוך.

8

דוגמה פופולרית בטופולוגיה: דפורמציה רציפה (הומוטופיה) בין ספל קפה וכעך שמדגימה כי שני הגופים הומיאומורפים, לשניהם טופולוגיה של טורוס. למעשה כדי ששני גופים יהיו הומיאומורפים אין צורך בדפורמציה רציפה, מספיק מיפוי והיפוך רציפים. המעבר בין הכעך לספל אינו אלא ארגון מחדש של היריעה מסביב לחור שבכעך בעזרת כיווץ ומתיחה מבלי לקרוע אותה או לחבר חלקים שלא היו מחוברים קודם.

9

פרוק פרדוקסלי של גרף קיילי של החבורה $F_{2}$ (החבורה החופשית עם 2 יוצרים). האנימציה מראה איך לפרק את הגרף למספר חלקים ולהרכיב מהם 2 העתקים של הגרף המקורי. פרוק כזה נקרא פרוק פרדוקסלי. בפני עצמו, פרוק זה אינו מפתיע יותר מהמלון של הילברט, אולם ניתן להסיק ממנו את משפט בנך-טרסקי (הנקרא לעיתים פרדוקס בנך-טרסקי) הקובע כי קיים פרוק פרדוקסלי של הכדור.

10

אנימציה המדגימה את הרעיון העומד מאחורי משולש פסקל המאפשר חישוב של המקדמים הבינומיים.

11

טורוס הנו גוף סיבוב הנוצר מסיבובו של מעגל סביב לציר הניצב לו אך לא חותך אותו. בתמונה מופיע טורוס עם חור ההולך וגדל עד שהטורוס "בולע" את עצמו.

12

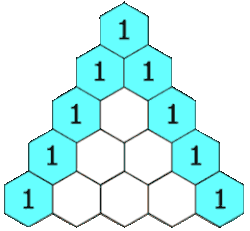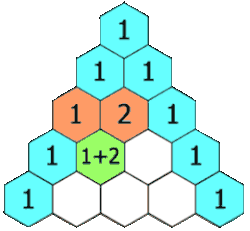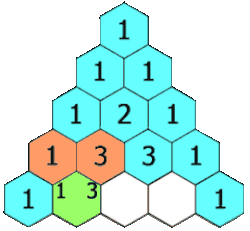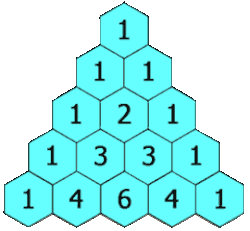
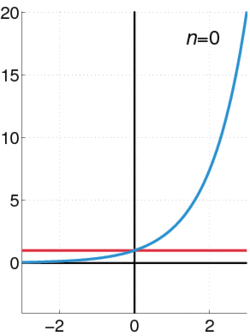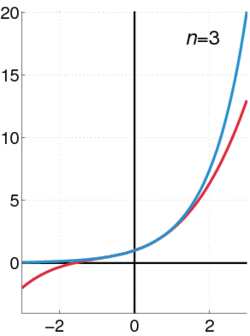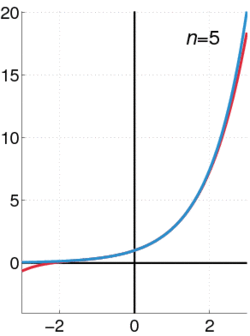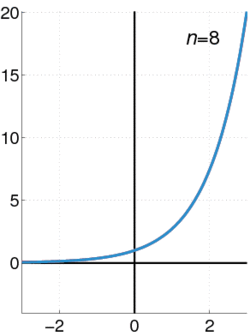
קירוב של הפונקציה $e^{x}\,$ לפולינום מדרגה n באמצעות פיתוח לטור מקלורן.

13

משפט פיתגורס, הוא אחד מהמשפטים הגאומטריים הנודעים ביותר. הוא קובע שסכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר-זווית, שווה לשטח הריבוע הבנוי על היתר. באנימציה רואים את אחת מההוכחות הרבות למשפט. בעזרת חיתוך ל-4 משולשים ישרי זווית וסידור החלקים מחדש מתקבלת הוכחה של המשפט.

14

מציאת כל המספרים הראשוניים בין 2 ל-120 באמצעות הנפה של ארטוסתנס.