קוואדרטריקס
קוואדרטריקס הוא עקום המוגדר באופן הדינמי הבא:
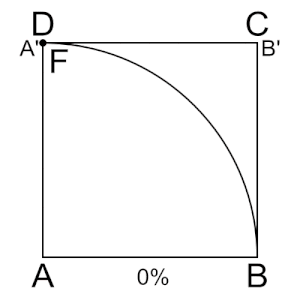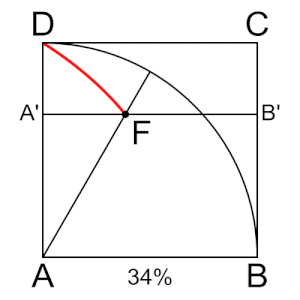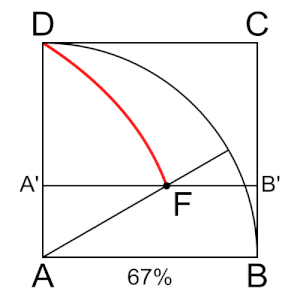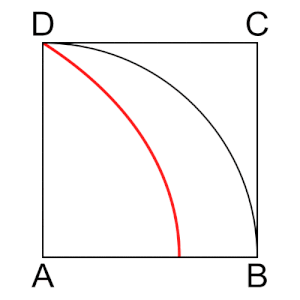

- בריבוע ABCD הצלע CD נעה במהירות קבועה לעבר הצלע המקבילה לה AB. באותו זמן הצלע AD נעה במהירות זוויתית קבועה סביב הציר A לעבר הצלע AB. המקום הגאומטרי של נקודות החיתוך של שתי הצלעות הנעות הללו הוא הקוואדרטריקס של היפיאס.
הפילוסוף היווני פרוקלוס מייחס את יצירת הקוואדרטריקס להיפיאס מאליס. הקוואדרטריקס קרוי לעיתים "הקוואדרטריקס של היפיאס".
הקוואדרטריקס אינו ניתן לבנייה באמצעים הסטנדרטיים של הגאומטריה, סרגל ומחוגה, אך כבר המתמטיקאים של יוון העתיקה גילו בו עניין, משום שכאשר עומד לרשותנו קוואדרטריקס, ניתן לפתור באמצעותו שתיים מהבעיות הגאומטריות של ימי קדם:
- שילוש זווית: חלוקת זווית נתונה לשלושה חלקים שווים
- תרבוע העיגול: בניית ריבוע השווה בשטחו לעיגול נתון.
שתי בעיות אלה העסיקו מתמטיקאים במשך כאלפיים שנה, ורק במאה ה-19 הוכח שהן לא פתירות, כלומר אין דרך לבצע את הבניות הנדרשות. חוסר היכולת לפתור בעיות אלה הוביל להמצאת כלים שיאפשרו את פתרונן, ובהם הקוואדרטריקס.
במערכת צירים קרטזית, שבה ABCD הוא ריבוע יחידה שקודקודו A נמצא בראשית הצירים, המשוואה של הקוואדרטריקס היא .
מהגדרת הקוואדרטריקס נובע שהיחס בין שתי זוויות שקודקודן A וקרן אחת שלהן היא הצלע AB, שווה ליחס שבין גובהי נקודת החיתוך של הקרן האחרת עם הקוואדרטריקס. כדי לחלק זווית כזו לשלושה חלקים שווים, די בהעברת מקביל לצלע AB בגובה השווה לשליש הגובה של נקודת החיתוך של הקרן האחרת. נקודת החיתוך של מקביל זה עם הקוואדרטריקס נותנת את הנקודה שדרכה תעבור הקרן האחרת של הזווית השווה לשליש הזווית הנתונה. בציור שמשמאל, לחלוקת הזווית EAB לשלושה חלקים שווים, יש לחלק את הקטע GF לשלושה חלקים שווים, ולהעביר מקביל לצלע AB דרך הנקודה שבשליש הגובה של GF.
על-פי המתמטיקאי היווני פפוס, המתמטיקאי היווני דינוסטרטוס השתמש בקוואדרטריקס לתרבוע העיגול.
לקריאה נוספת
עריכה- בנו ארבל, קיצור תולדות המתמטיקה, מכון מופ"ת, 2005, עמ' 107-109.
