קיפול נייר לשניים

האתגר של קיפול נייר לשניים מספר פעמים רב, משמש כהדגמה פופולרית לקצב גידול מעריכי. צורה נפוצה של האתגר היא ניסיון לקפל דף נייר בגודל רגיל 10 פעמים לשניים קיפול אחרי קיפול מבלי לפתוח את הקיפולים. ניסיון לעשות זאת נתקע לאחר 6–8 קיפולים בהתאם לסוג הנייר. ברור שאם מגדילים את הנייר מספיק או משתמשים בנייר דק מספיק אז ניתן לקפל (לפחות באופן תאורטי) כל מספר קיפולים. היוריסטיקה פשוטה מראה כי אם מגדילים את הנייר פי 8 בקירוב (או לחלופין הופכים אותו לדק פי 8) אז ניתן להוסיף עוד שני קיפולים.

תרשים של נייר המקופל בכיוון אחד ארבע פעמים

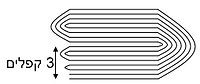
בשנת 2001 הוכיחה והדגימה תלמידת תיכון בשם בריטני גאליוון (Britney Gallivan) (ילידת 1985) את ההתנהגות של קיפול גיליון לשניים. גאליוון פיתחה נוסחה למספר הקיפולים שניתן לבצע בהינתן גודל ועובי הנייר. הנוסחה התבססה על מודל פשטני אך מדויק למדי של התנהגות הנייר בעת קיפול. גאליוון אף השיגה גיליון גדול דיו של נייר וקיפלה אותו לשניים 12 פעמים.

פתרון הבעיה

בריטני גאליוון

תמונה זו מוצגת בוויקיפדיה בשימוש הוגן.
נשמח להחליפה בתמונה חופשית.

גאליוון פתרה את הבעיה בעקבות שאלת אתגר אשר ניתנה לה בשיעור מתמטיקה בתיכון - לקפל נייר 12 פעמים. גאליוון, בניסיון להבין את הגורם המקשה על הקיפול, ניסחה את המשוואה המתמטית המתארת את התנאי המגביל קיפול של נייר בעובי t בכיוון אחד, n פעמים. היא הדגימה כי אורך הנייר המינימלי, L, הדרוש לשם הקיפול ניתן על ידי המשוואה: $L={\frac {\pi t}{6}}(2^{n}+4)(2^{n}-1)$.

לאחר פתרון המשוואה היא הדגימה את הפתרון הלכה למעשה ובתחילת 2002 קיפלה נייר טואלט באורך 1200 מטרים 12 פעמים.

גאליוון אף ניסחה את הגורם המגביל קיפול נייר בעובי t בכיוונים מנוגדים מספר פעמים השווה ל-n וגילתה שבקירוב רוחב הנייר המינימלי, W, הדרוש לשם כך הוא: $W=\pi t2^{{\frac {3}{2}}\left(n-1\right)}$.

סדרי גודל בקיפול מרובה

מכיוון ש-$\ 0.1\cdot 2^{42}$ מילימטרים הם יותר מ-400,000 קילומטרים, קיפול של דף נייר בעובי 0.1 מ"מ 42 פעמים ייצור ערימה שגובהה גדול מהמרחק בין כדור הארץ לירח. לפי הנוסחה של גאליוון, אורך הנייר הדרוש לסדרת קיפולים כזו הוא כ-$\ 10^{18}$ קילומטרים, שהם כ-10,000 פעמים המרחק לאלפא קנטאורי ובחזרה.

הנוסחה של גובה הנייר אחרי N קיפולים

N=מספר הקיפולים

T=עובי הדף

X=גובה הדף שייווצר

$X=T\cdot 2^{N}$

הגעה לגובה מסוים

כדי להגיע לגובה ספציפי בעזרת קיפולי נייר מסוג זה אפשר להיעזר בנוסחה הבאה: נשתמש באותם משתנים מהפסקה הקודמת (ה-X וה-T באותן יחידות מידה).

$N=log_{2}(X/T)$

דוגמאות

אם ניקח דף רגיל בעובי של 0.05 מ"מ ונקפל אותו 15 פעמים הוא יהיה בגובה מטר וחצי בערך.

אחרי 24 פעמים 800 מטר.

אחרי 43 פעמים נגיע לירח.

אחרי 52 פעמים נגיע לשמש ונוכל לחזור גם חצי דרך חזרה.

אחרי 84 פעמים הגובה יהיה יותר גדול מהקוטר של הגלקסיה שלנו.

ראו גם

• מתמטיקה של קיפולי נייר
• אוריגמי

לקריאה נוספת

• Britney C. Gallivan, How to fold paper in half twelve times (an "impossible challenge" solved and explained), Historical Society of Pomona Valley, Pomona California, 2002

קישורים חיצוניים

• האגודה ההיסטורית של פומונה
• אתר על המתמטיקה של קיפולי נייר
• ההוכחה במלואה
• סרטון של TED-ed על הנושא, סרטון באתר יוטיוב (באנגלית)