במתמטיקה , sinc (קיצור של sine cardinal ), שמסומנת
s
i
n
c
(
x
)
{\displaystyle \mathrm {sinc} (x)\,}
פונקציה המוגדרת בדרך כלל כך:
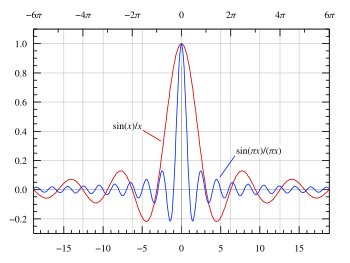
פונקציית ה-sinc המנורמלת (בכחול ) ופונקציית ה-sinc הלא-מנורמלת (באדום ) מוצגות על אותה סקלה עבור
−
6
π
≤
x
≤
6
π
{\displaystyle \ -6\pi \leq x\leq 6\pi }
s
i
n
c
(
x
)
=
sin
(
x
)
x
{\displaystyle \mathrm {sinc} (x)={\frac {\sin(x)}{x}}}
בעיבוד אותות דיגיטלי ותורת האינפורמציה , נעשה לרוב שימוש בפונקציית ה-sinc המנורמלת , המוגדרת כך:
s
i
n
c
(
x
)
=
sin
(
π
x
)
π
x
{\displaystyle \mathrm {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}}
בשני המקרים, ערך הפונקציה בנקודת אי-הרציפות הסליקה
x
=
0
{\displaystyle \ x=0}
גבול שאליו שואפת הפונקציה, כלומר, ל-1. ראו עוד בנושא: הגבול של sin(x)/x .
לפונקציית ה-sinc המנורמלת יש תכונות שהופכות אותה לאידיאליות ביחס לאינטרפולציות ופונקציות בעלות רוחב פס מוגבל (Bandlimited functions ):
s
i
n
c
(
0
)
=
1
{\displaystyle \mathrm {sinc} (0)=1\,}
s
i
n
c
(
k
)
=
0
{\displaystyle \mathrm {sinc} (k)=0\,}
k
≠
0
{\displaystyle k\neq 0\,}
k
∈
Z
{\displaystyle k\in \mathbb {Z} \,}
מספר שלם שונה מאפס); כלומר, זו פונקציית אינטרפולציה.הפונקציות
x
k
(
t
)
=
s
i
n
c
(
t
−
k
)
{\displaystyle x_{k}(t)=\mathrm {sinc} (t-k)\ }
בסיס אורתונורמלי עבור פונקציות בעלות רוחב פס מוגבל במרחב הפונקציות
L
2
(
R
)
{\displaystyle L^{2}(\mathbb {R} )}
תדירות זוויתית מקסימלית
ω
H
=
π
{\displaystyle \omega _{\mathrm {H} }=\pi \,}
f
H
=
1
/
2
{\displaystyle f_{\mathrm {H} }=1/2\,}
תכונות נוספות של פונקציית ה-sinc:
נקודות הקיצון של פונקציית ה-sinc הלא-מנורמלת
sin
(
x
)
x
{\displaystyle {\frac {\sin(x)}{x}}\,}
קוסינוס . כלומר
sin
(
x
)
x
=
cos
(
x
)
{\displaystyle {\frac {\sin(x)}{x}}=\cos(x)\,}
נגזרת של
sin
(
x
)
x
{\displaystyle {\frac {\sin(x)}{x}}\,}
פונקציית ה-sinc הלא-מנורמלת היא פונקציית בסל כדורית מסדר 0 והסוג הראשון,
j
0
(
x
)
=
sin
(
x
)
x
{\displaystyle j_{0}(x)={\frac {\sin(x)}{x}}\,}
j
0
(
π
x
)
{\displaystyle j_{0}(\pi x)\,}
האפסים של פונקציית ה-sinc הלא-מנורמלת הם כפולות (שונות מאפס) של פאי (
π
{\displaystyle \pi \,}
s
i
n
c
(
x
)
=
sin
(
π
x
)
π
x
{\displaystyle \mathrm {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}\,}
התמרת פורייה הרציפה של פונקציית ה-sinc המנורמלת
s
i
n
c
(
x
)
=
sin
(
π
x
)
π
x
{\displaystyle \mathrm {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}\,}
r
e
c
t
(
f
)
{\displaystyle \mathrm {rect} (f)\,}
∫
−
∞
∞
s
i
n
c
(
t
)
e
−
2
π
i
f
t
d
t
=
r
e
c
t
(
f
)
{\displaystyle \int _{-\infty }^{\infty }\mathrm {sinc} (t)\,e^{-2\pi ift}\,\mathrm {d} t=\mathrm {rect} (f)}
כאשר פונקציית המלבן היא 1 עבור ארגומנט בין 1/2 ל 1/2- ואפס אחרת. אינטגרל פורייה לעיל, כולל את המקרה הפרטי
∫
−
∞
∞
sin
(
π
x
)
π
x
d
x
=
r
e
c
t
(
0
)
=
1
{\displaystyle \int _{-\infty }^{\infty }{\frac {\sin(\pi x)}{\pi x}}\,\mathrm {d} x=\mathrm {rect} (0)=1}
הוא אינטגרל לא-אמיתי . זהו אינו אינטגרל לבג כיוון ש-:
∫
−
∞
∞
|
sin
(
π
x
)
π
x
|
d
x
=
∞
{\displaystyle \int _{-\infty }^{\infty }\left|{\frac {\sin(\pi x)}{\pi x}}\right|\,\mathrm {d} x=\infty }
s
i
n
c
(
x
)
=
sin
(
π
x
)
π
x
=
∏
n
=
1
∞
(
1
−
x
2
n
2
)
{\displaystyle \mathrm {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{n^{2}}}\right)}
s
i
n
c
(
x
)
=
sin
(
π
x
)
π
x
=
1
Γ
(
1
+
x
)
Γ
(
1
−
x
)
{\displaystyle \mathrm {sinc} (x)={\frac {\sin(\pi x)}{\pi x}}={\frac {1}{\Gamma (1+x)\Gamma (1-x)}}}
כאשר
Γ
(
x
)
{\displaystyle \Gamma (x)}
פונקציית גמא .
∫
0
x
sin
(
θ
)
θ
d
θ
=
S
i
(
x
)
{\displaystyle \int _{0}^{x}{\frac {\sin(\theta )}{\theta }}\,\mathrm {d} \theta =\mathrm {Si} (x)}
כאשר (Si(x הוא אינטגרל סינוס (sine integral ).
s
i
n
c
(
x
)
=
e
i
x
−
e
−
i
x
2
i
x
{\displaystyle \mathrm {sinc} (x)={\frac {e^{ix}-e^{-ix}}{2ix}}\,}
עריכה
אף על פי שהיא אינה התפלגות , פונקציית ה-sinc המנורמלת יכולה לשמש לייצוג פונקציית דלתא של דיראק
δ
(
x
)
{\displaystyle \ \delta (x)}
lim
a
→
0
1
a
sinc
(
x
/
a
)
=
δ
(
x
)
{\displaystyle \lim _{a\rightarrow 0}{\frac {1}{a}}{\textrm {sinc}}(x/a)=\delta (x)}
זה אינו גבול רגיל, משום שאגף שמאל לא מתכנס. עם זאת, מתקיים:
lim
a
→
0
∫
−
∞
∞
1
a
sinc
(
x
/
a
)
φ
(
x
)
d
x
=
φ
(
0
)
,
{\displaystyle \lim _{a\rightarrow 0}\int _{-\infty }^{\infty }{\frac {1}{a}}{\textrm {sinc}}(x/a)\varphi (x)\,\mathrm {d} x=\varphi (0),}
לכל פונקציה חלקה
φ
(
x
)
{\displaystyle \varphi (x)}
תומך קומפקטי .
בביטוי לעיל, כש-a שואף לאפס, מספר התנודות עבור אורך יחידה של פונקציית ה-sinc שואף לאינסוף . אף על פי כן, הביטוי תמיד מתנודד בתוך מעטפת של
±
1
/
(
π
x
)
{\displaystyle \ \pm 1/(\pi x)}
δ
(
x
)
{\displaystyle \ \delta (x)}
פונקציה ולא כהתפלגות . פתרון דומה נמצא בתופעת גיבס .