ויקיפדיה:ערכים מומלצים/המלצות קודמות/ינואר 2009

ינואר
1 בינואר 2009	גאיוס מריוס (157 לפנה"ס – 13 בינואר 86 לפנה"ס) היה מצביא ומדינאי רומי, המנצח של מלחמת יוגורתה ומלחמת הקימברים והטווטונים. גאיוס מריוס היה מחדש צבאי ומנהיג הסיעה הפופולרית ברומא. מריוס היה האדם היחידי בתולדות הרפובליקה הרומית שנבחר שבע פעמים למשרת הקונסול. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
2 בינואר 2009	גאיוס מריוס (157 לפנה"ס – 13 בינואר 86 לפנה"ס) היה מצביא ומדינאי רומי, המנצח של מלחמת יוגורתה ומלחמת הקימברים והטווטונים. גאיוס מריוס היה מחדש צבאי ומנהיג הסיעה הפופולרית ברומא. מריוס היה האדם היחידי בתולדות הרפובליקה הרומית שנבחר שבע פעמים למשרת הקונסול. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
3 בינואר 2009	המראה מגבעת בירסה שניצבה במרכזה של העיר העיר קרתגו, שנקראה בשפה הפיניקית קרת חדת, או "עיר חדשה", שוכנת לחופו של הים התיכון בשטח העירוני הבנוי של העיר תוניס, בירת תוניסיה. אתרי העיר מהתקופה הפונית לא השתמרו בצורה טובה, בין היתר בשל ההרס הרומי השיטתי לאחר המלחמה הפונית השלישית, אך ממצאים רבים יותר נשתמרו מתקופת היישוב הרומי, אשר המשיך והתקיים גם לאחר שהרומאים נדחקו מצפון אפריקה. בשל חשיבותו ההיסטורית והתרבותית מוכרז המקום כאתר מורשת עולמית מאז שנת 1979. מקובל שהעיר נוסדה על ידי הפיניקים במאה ה-9 לפנה"ס על חצי אי קטן לחופיו הדרומיים של מצר סיציליה, המפריד בין אגנו המזרחי ואגנו המערבי של הים התיכון. העיר הוקפה בחומה באורך של 37 ק"מ, שבוצרה וחוזקה בעיקר לאורך קטע בן חמישה קילומטרים בצידה המערבי הפונה אל מצר היבשה, והגיעה לשיאה החל במאה ה-5 לפנה"ס. היא נחרבה עד היסוד בשנת 146 לפנה"ס על ידי הרומאים, שמאוחר יותר הקימו באתר עיר משגשגת משלהם. סופה המוחלט של קרתגו בא לה מידי הערבים בסוף המאה ה-7, והיא נבלעה על ידי המטרופולין של תוניס הסמוכה במהלך המאה ה-20. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
4 בינואר 2009	המראה מגבעת בירסה שניצבה במרכזה של העיר העיר קרתגו, שנקראה בשפה הפיניקית קרת חדת, או "עיר חדשה", שוכנת לחופו של הים התיכון בשטח העירוני הבנוי של העיר תוניס, בירת תוניסיה. אתרי העיר מהתקופה הפונית לא השתמרו בצורה טובה, בין היתר בשל ההרס הרומי השיטתי לאחר המלחמה הפונית השלישית, אך ממצאים רבים יותר נשתמרו מתקופת היישוב הרומי, אשר המשיך והתקיים גם לאחר שהרומאים נדחקו מצפון אפריקה. בשל חשיבותו ההיסטורית והתרבותית מוכרז המקום כאתר מורשת עולמית מאז שנת 1979. מקובל שהעיר נוסדה על ידי הפיניקים במאה ה-9 לפנה"ס על חצי אי קטן לחופיו הדרומיים של מצר סיציליה, המפריד בין אגנו המזרחי ואגנו המערבי של הים התיכון. העיר הוקפה בחומה באורך של 37 ק"מ, שבוצרה וחוזקה בעיקר לאורך קטע בן חמישה קילומטרים בצידה המערבי הפונה אל מצר היבשה, והגיעה לשיאה החל במאה ה-5 לפנה"ס. היא נחרבה עד היסוד בשנת 146 לפנה"ס על ידי הרומאים, שמאוחר יותר הקימו באתר עיר משגשגת משלהם. סופה המוחלט של קרתגו בא לה מידי הערבים בסוף המאה ה-7, והיא נבלעה על ידי המטרופולין של תוניס הסמוכה במהלך המאה ה-20. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
5 בינואר 2009	קרס עצם, תקופת האבן, שוודיה דיג – ציד בעלי חיים ימיים לשם מזון, ספורט או תחביב. דיג מבוצע במקומות שונים: נהרות, תעלות, אגמים, ימים ואוקיינוסים. דיג מתבצע מהחוף, מסירה או מאנייה, על ידי אדם בודד או כפעילות משותפת של קבוצת אנשים. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
6 בינואר 2009	קרס עצם, תקופת האבן, שוודיה דיג – ציד בעלי חיים ימיים לשם מזון, ספורט או תחביב. דיג מבוצע במקומות שונים: נהרות, תעלות, אגמים, ימים ואוקיינוסים. דיג מתבצע מהחוף, מסירה או מאנייה, על ידי אדם בודד או כפעילות משותפת של קבוצת אנשים. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
7 בינואר 2009	מאיר טוביאנסקי (20 במאי 1904 – 30 ביוני 1948) ישראלי שהואשם בריגול נגד ישראל על לא עוול בכפו במהלך מלחמת העצמאות. טוביאנסקי הועמד בפני בית דין שדה צה"לי, הורשע והוצא להורג. מאוחר יותר טוהר שמו. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
8 בינואר 2009	מאיר טוביאנסקי (20 במאי 1904 – 30 ביוני 1948) ישראלי שהואשם בריגול נגד ישראל על לא עוול בכפו במהלך מלחמת העצמאות. טוביאנסקי הועמד בפני בית דין שדה צה"לי, הורשע והוצא להורג. מאוחר יותר טוהר שמו. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
9 בינואר 2009	סנט קילדה הוא ארכיפלג מבודד השוכן בצפון האוקיינוס האטלנטי במרחק של 64 ק"מ מצפון-מערב לאי ויסט הצפוני. בארכיפלג נכללים האיים המערביים ביותר בהברידים החיצוניים של סקוטלנד. האי הגדול ביותר בארכיפלג הוא הירטה, והצוקים הנמצאים בו הם הגבוהים ביותר בממלכה המאוחדת. האוכלוסייה דוברת הגאלית מונה לכל היותר 100 תושבים, כבר מאז 1851. מקורו של השם סנט קילדה מהווה כר להשערות רבות. המורשת האנושית באיים מאופיינת במספר אלמנטים אדריכליים ייחודיים מהתקופות ההיסטורית והפרהיסטורית, למרות שהתיעודים הקדומים ביותר של יישוב אנושי במקום מתוארכים לימי הביניים. הכפר הימי-ביניימי בהירטה נבנה מחדש במהלך המאה ה-19, אך השפעות הדת, התיירות ומלחמת העולם הראשונה הובילו לפינויו של האי ב-1930. כיום האיים מאוכלסים על ידי אנשי הכוחות המזוינים של בריטניה. סיפורו של סנט קילדה משך תשומת לב אמנותית, ובין השאר נכתבה אופרה בנושא. סנט קילדה הפך לאתר המורשת העולמית הראשון בסקוטלנד והוא אחד מהאתרים הבודדים שהוכרזו כאתרים מעורבים, בשל איכויותיו הטבעיות, הימיות והתרבותיות. האיים משמשים כאתר קינון חשוב למספר מינים של עופות ימיים ובהם סולה צפונית ותוכי ים אטלנטי. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
10 בינואר 2009	סנט קילדה הוא ארכיפלג מבודד השוכן בצפון האוקיינוס האטלנטי במרחק של 64 ק"מ מצפון-מערב לאי ויסט הצפוני. בארכיפלג נכללים האיים המערביים ביותר בהברידים החיצוניים של סקוטלנד. האי הגדול ביותר בארכיפלג הוא הירטה, והצוקים הנמצאים בו הם הגבוהים ביותר בממלכה המאוחדת. האוכלוסייה דוברת הגאלית מונה לכל היותר 100 תושבים, כבר מאז 1851. מקורו של השם סנט קילדה מהווה כר להשערות רבות. המורשת האנושית באיים מאופיינת במספר אלמנטים אדריכליים ייחודיים מהתקופות ההיסטורית והפרהיסטורית, למרות שהתיעודים הקדומים ביותר של יישוב אנושי במקום מתוארכים לימי הביניים. הכפר הימי-ביניימי בהירטה נבנה מחדש במהלך המאה ה-19, אך השפעות הדת, התיירות ומלחמת העולם הראשונה הובילו לפינויו של האי ב-1930. כיום האיים מאוכלסים על ידי אנשי הכוחות המזוינים של בריטניה. סיפורו של סנט קילדה משך תשומת לב אמנותית, ובין השאר נכתבה אופרה בנושא. סנט קילדה הפך לאתר המורשת העולמית הראשון בסקוטלנד והוא אחד מהאתרים הבודדים שהוכרזו כאתרים מעורבים, בשל איכויותיו הטבעיות, הימיות והתרבותיות. האיים משמשים כאתר קינון חשוב למספר מינים של עופות ימיים ובהם סולה צפונית ותוכי ים אטלנטי. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
11 בינואר 2009	מנורת הכנסת "מנורת הכנסת" היא אנדרטת ברונזה בגובה כחמישה מטרים, הניצבת בקצה גן הוורדים, מול משכן הכנסת בירושלים. את המנורה העניק הפרלמנט הבריטי כמחווה למדינת ישראל הצעירה בשנת 1956, והיא מעשה ידיו של בֶּנוֹ אֶלְקָן, אמן יהודי-בריטי ממוצא גרמני, שעמל עליה במשך שש שנים. המנורה מציגה כשלושים אירועים, ביטויים, דמויות ומושגים מכוננים בתולדות עם ישראל, ונחשבת ל"ספר לימוד" ויזואלי של ההיסטוריה היהודית לדורותיה. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
12 בינואר 2009	מנורת הכנסת "מנורת הכנסת" היא אנדרטת ברונזה בגובה כחמישה מטרים, הניצבת בקצה גן הוורדים, מול משכן הכנסת בירושלים. את המנורה העניק הפרלמנט הבריטי כמחווה למדינת ישראל הצעירה בשנת 1956, והיא מעשה ידיו של בֶּנוֹ אֶלְקָן, אמן יהודי-בריטי ממוצא גרמני, שעמל עליה במשך שש שנים. המנורה מציגה כשלושים אירועים, ביטויים, דמויות ומושגים מכוננים בתולדות עם ישראל, ונחשבת ל"ספר לימוד" ויזואלי של ההיסטוריה היהודית לדורותיה. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
13 בינואר 2009	פרס פרס, סוג עוף דורס ממשפחת הנציים ולו מין יחיד. בישראל מובחן כאחד ממיני הנשרים של העולם הישן (קבוצה לא טקסונומית של אוכלי פגרים). מקור השם בעברית מהתנ"ך, שם מוזכר כאחד העופות הטמאים למאכל. יש הטוענים כי הפרס המוזכר בתנ"ך הוא בעצם עיט. באנגלית מכונה Bearded Vulture בשל הניצוי הייחודי בפניו – מהעין עד למקור, המקנה לפניו צורת שפם וזקן. נקרא גם Lammergeier באנגלית ובגרמנית שמשמעו "עיט הטלאים" ובעבר Ossifrage שמשמעו "שובר עצמות". לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
14 בינואר 2009	פרס פרס, סוג עוף דורס ממשפחת הנציים ולו מין יחיד. בישראל מובחן כאחד ממיני הנשרים של העולם הישן (קבוצה לא טקסונומית של אוכלי פגרים). מקור השם בעברית מהתנ"ך, שם מוזכר כאחד העופות הטמאים למאכל. יש הטוענים כי הפרס המוזכר בתנ"ך הוא בעצם עיט. באנגלית מכונה Bearded Vulture בשל הניצוי הייחודי בפניו – מהעין עד למקור, המקנה לפניו צורת שפם וזקן. נקרא גם Lammergeier באנגלית ובגרמנית שמשמעו "עיט הטלאים" ובעבר Ossifrage שמשמעו "שובר עצמות". לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
15 בינואר 2009	פסלו של אמידה בודהה מברוזנה (1252 לספירה) יצירות אמנות נוצרו ביפן מראשית ההתיישבות בה (כעשרת אלפים שנה לפנה"ס) ועד לימינו. במשך הדורות התפתחה אמנות יפנית בעלת מאפיינים ייחודיים. ההיסטוריה היפנית שזורה בפרקי זמן קצרים שבמהלכם חדרו אל הארץ השפעות תרבותיות זרות לרוב, וביניהם תקופות ארוכות של ניתוק וחוסר קשר עם העולם החיצוני. עם הזמן למדו היפנים לחקות ולהטמיע את היסודות הזרים שחלחלו אל ארצם ואלו השתלבו בתרבות האסתטית של יפן. האמנות היפנית המורכבת המוקדמת ביותר נוצרה במאה ה-7 וה-8 והיא ספוגה בהשפעות בודהיסטיות. במאה ה-9, עת צימצמו היפנים את הזיקה לסין והחלו לפתח תרבות עצמאית, גדלה חשיבותן של האמנויות החילוניות, אם כי גם האמנות הדתית לא נזנחה עד המאה ה-15. לאחר מלחמת אונין (1467-1477) נכנסה יפן לתקופת תוהו ובוהו פוליטי, חברתי וכלכלי שנמשך כמעט מאה שנים. במדינה כפי שהתעצבה תחת הנהגתם של שוגוני הטוקוגאווה, היה לדת המאורגנת תפקיד פחות בהרבה בחיי העם, והאמנויות ששרדו היו בעיקר חילוניות. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
16 בינואר 2009	פסלו של אמידה בודהה מברוזנה (1252 לספירה) יצירות אמנות נוצרו ביפן מראשית ההתיישבות בה (כעשרת אלפים שנה לפנה"ס) ועד לימינו. במשך הדורות התפתחה אמנות יפנית בעלת מאפיינים ייחודיים. ההיסטוריה היפנית שזורה בפרקי זמן קצרים שבמהלכם חדרו אל הארץ השפעות תרבותיות זרות לרוב, וביניהם תקופות ארוכות של ניתוק וחוסר קשר עם העולם החיצוני. עם הזמן למדו היפנים לחקות ולהטמיע את היסודות הזרים שחלחלו אל ארצם ואלו השתלבו בתרבות האסתטית של יפן. האמנות היפנית המורכבת המוקדמת ביותר נוצרה במאה ה-7 וה-8 והיא ספוגה בהשפעות בודהיסטיות. במאה ה-9, עת צימצמו היפנים את הזיקה לסין והחלו לפתח תרבות עצמאית, גדלה חשיבותן של האמנויות החילוניות, אם כי גם האמנות הדתית לא נזנחה עד המאה ה-15. לאחר מלחמת אונין (1467-1477) נכנסה יפן לתקופת תוהו ובוהו פוליטי, חברתי וכלכלי שנמשך כמעט מאה שנים. במדינה כפי שהתעצבה תחת הנהגתם של שוגוני הטוקוגאווה, היה לדת המאורגנת תפקיד פחות בהרבה בחיי העם, והאמנויות ששרדו היו בעיקר חילוניות. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
17 בינואר 2009	חידות חיתוך והרכבה הן חידות העוסקות בדרכים שבהן ניתן לחתוך צורה למספר צורות אחרות, לדרכים שבהן ניתן לקחת חלקים ולחבר אותם יחד לצורה חדשה, וכן בחידות המשלבות את שתי הפעולות: כיצד ניתן לחתוך צורה נתונה על מנת להרכיב צורה אחרת מחלקיה. חידת חיתוך קלאסית חידת חיתוך קלאסית היא כיצד ניתן לחלק את הצורה הנקראת L-tromino לשניים, שלושה וארבעה חלקים זהים (בתמונה נראה הפתרון לחלוקה ל-4 חלקים). חידת ההרכבה המפורסמת ביותר היא הטנגרם, ובה ריבוע מחולק ל-7 חלקים שמהם ניתן להרכיב מגוון רב של צורות הכוללות אנשים, בעלי חיים וצמחים. חידה דומה מסוג זה, הנקראת 'סטומכיוון' נחקרה על ידי המדען והמתמטיקאי היווני ארכימדס. המתמטיקאי ההודי הגדול אריאבהטה השתמש בשיטות של חיתוך והרכבה על מנת להוכיח את משפט פיתגורס (הוכחה שנלמדת עד היום בבתי הספר) ולאחריו הופיעו הוכחות רבות נוספות המשתמשות גם הן בחיתוך והרכבה. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
18 בינואר 2009	חידות חיתוך והרכבה הן חידות העוסקות בדרכים שבהן ניתן לחתוך צורה למספר צורות אחרות, לדרכים שבהן ניתן לקחת חלקים ולחבר אותם יחד לצורה חדשה, וכן בחידות המשלבות את שתי הפעולות: כיצד ניתן לחתוך צורה נתונה על מנת להרכיב צורה אחרת מחלקיה. חידת חיתוך קלאסית חידת חיתוך קלאסית היא כיצד ניתן לחלק את הצורה הנקראת L-tromino לשניים, שלושה וארבעה חלקים זהים (בתמונה נראה הפתרון לחלוקה ל-4 חלקים). חידת ההרכבה המפורסמת ביותר היא הטנגרם, ובה ריבוע מחולק ל-7 חלקים שמהם ניתן להרכיב מגוון רב של צורות הכוללות אנשים, בעלי חיים וצמחים. חידה דומה מסוג זה, הנקראת 'סטומכיוון' נחקרה על ידי המדען והמתמטיקאי היווני ארכימדס. המתמטיקאי ההודי הגדול אריאבהטה השתמש בשיטות של חיתוך והרכבה על מנת להוכיח את משפט פיתגורס (הוכחה שנלמדת עד היום בבתי הספר) ולאחריו הופיעו הוכחות רבות נוספות המשתמשות גם הן בחיתוך והרכבה. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
19 בינואר 2009	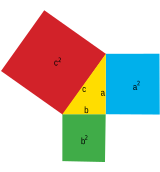משפט פיתגורס הוא משפט בגאומטריה, והוא אחד המשפטים המתמטיים הנודעים ביותר. הוא קובע שסכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר-זווית, שווה לשטח הריבוע הבנוי על היתר (הניצבים הם שתי צלעות הזווית הישרה, והיתר הוא הצלע הארוכה של המשולש). בניסוח פורמלי: אם אורכי הניצבים במשולש ישר-זווית הם $\ a$ ו-$\ b$, ואורך היתר הוא $\ c$, אז: $\ a^{2}+b^{2}=c^{2}$. המשפט ההפוך, הקובע שמשולש שבו ריבוע צלע אחת שווה לסכום ריבועי הצלעות האחרות הוא ישר-זווית, נכון גם הוא. המשפט נקרא על שם המתמטיקאי והפילוסוף היווני פיתגורס, שחי במאה ה-6 לפנה"ס, על אף שהמשפט היה מוכר בתרבויות עתיקות מאות שנים לפני זמנו. בעיה מפורסמת מתורת המספרים היא מציאת משולשים ישרי זווית שאורכי הצלעות שלהם הם מספרים שלמים, כלומר למצוא פתרונות שלמים למשוואה הדיופנטית: $\ a^{2}+b^{2}=c^{2}$. שלשה של מספרים כאלה קרויה שלשה פיתגורית, וידוע שיש אינסוף שלשות מסוג זה. השלשה 3, 4, 5 היא דוגמה לשלשה פיתגורית, שכן מספרים שלמים אלה מקיימים את המשוואה $\ (9+16=25)\quad 3^{2}+4^{2}=5^{2}\quad$. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
20 בינואר 2009	משפט פיתגורס הוא משפט בגאומטריה, והוא אחד המשפטים המתמטיים הנודעים ביותר. הוא קובע שסכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר-זווית, שווה לשטח הריבוע הבנוי על היתר (הניצבים הם שתי צלעות הזווית הישרה, והיתר הוא הצלע הארוכה של המשולש). בניסוח פורמלי: אם אורכי הניצבים במשולש ישר-זווית הם $\ a$ ו-$\ b$, ואורך היתר הוא $\ c$, אז: $\ a^{2}+b^{2}=c^{2}$. המשפט ההפוך, הקובע שמשולש שבו ריבוע צלע אחת שווה לסכום ריבועי הצלעות האחרות הוא ישר-זווית, נכון גם הוא. המשפט נקרא על שם המתמטיקאי והפילוסוף היווני פיתגורס, שחי במאה ה-6 לפנה"ס, על אף שהמשפט היה מוכר בתרבויות עתיקות מאות שנים לפני זמנו. בעיה מפורסמת מתורת המספרים היא מציאת משולשים ישרי זווית שאורכי הצלעות שלהם הם מספרים שלמים, כלומר למצוא פתרונות שלמים למשוואה הדיופנטית: $\ a^{2}+b^{2}=c^{2}$. שלשה של מספרים כאלה קרויה שלשה פיתגורית, וידוע שיש אינסוף שלשות מסוג זה. השלשה 3, 4, 5 היא דוגמה לשלשה פיתגורית, שכן מספרים שלמים אלה מקיימים את המשוואה $\ (9+16=25)\quad 3^{2}+4^{2}=5^{2}\quad$. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
21 בינואר 2009	מפת אזורי זמן שעון קיץ הוא השעון הרשמי הנהוג באזור זמן מוגדר למשך תקופה מסוימת בשנה, בדרך כלל מהאביב ועד הסתיו, בשונה מן השעון הרשמי הנהוג באותו מקום בשאר השנה, על פי זמן אוניברסלי מתואם, המכונה גם שעון חורף. השינוי מתבטא לרוב בהזזת השעון שעה אחת קדימה בתחילת התקופה ובהזזתו לאחור בסופה. שינוי השעה הרשמית באזור זמן מוגדר נעשה לשם ניצול טוב יותר של אור יום טבעי, וכדי להפחית את הצורך בתאורה מלאכותית. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
22 בינואר 2009	מפת אזורי זמן שעון קיץ הוא השעון הרשמי הנהוג באזור זמן מוגדר למשך תקופה מסוימת בשנה, בדרך כלל מהאביב ועד הסתיו, בשונה מן השעון הרשמי הנהוג באותו מקום בשאר השנה, על פי זמן אוניברסלי מתואם, המכונה גם שעון חורף. השינוי מתבטא לרוב בהזזת השעון שעה אחת קדימה בתחילת התקופה ובהזזתו לאחור בסופה. שינוי השעה הרשמית באזור זמן מוגדר נעשה לשם ניצול טוב יותר של אור יום טבעי, וכדי להפחית את הצורך בתאורה מלאכותית. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
23 בינואר 2009	מגדל המים החדש כפר סבא היא עיר במחוז המרכז בישראל. היא הוכרזה כעיר בשנת 1963. כפר סבא מוזכרת לראשונה בכתבי יוסף בן מתתיהו בתיאור מלחמותיו של המלך החשמונאי אלכסנדר ינאי. עדות לקיומו של יישוב יהודי בכפר סבא מאות שנים אחר כך, במאות ה־7 עד ה־9 לספירה יש מפסיפס שנחשף בבית הכנסת בתל רחוב שמדרום לבית שאן. בקטע המתאר קיום הלכות נזכר היישוב "כפר סבה" כאחד היישובים היהודיים בשרון. כיום מזהים את מיקום כפר־סבא של תקופת בית שני עם היישוב הערבי באותו שם שקם כנראה במאה ה-10 – באזור שיכון קפלן של היום. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
24 בינואר 2009	מגדל המים החדש כפר סבא היא עיר במחוז המרכז בישראל. היא הוכרזה כעיר בשנת 1963. כפר סבא מוזכרת לראשונה בכתבי יוסף בן מתתיהו בתיאור מלחמותיו של המלך החשמונאי אלכסנדר ינאי. עדות לקיומו של יישוב יהודי בכפר סבא מאות שנים אחר כך, במאות ה־7 עד ה־9 לספירה יש מפסיפס שנחשף בבית הכנסת בתל רחוב שמדרום לבית שאן. בקטע המתאר קיום הלכות נזכר היישוב "כפר סבה" כאחד היישובים היהודיים בשרון. כיום מזהים את מיקום כפר־סבא של תקופת בית שני עם היישוב הערבי באותו שם שקם כנראה במאה ה-10 – באזור שיכון קפלן של היום. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
25 בינואר 2009	דיוקנו המפורסם של הרמב"ם תמונתו של הרמב"ם היא דיוקן מפורסם של הרמב"ם, שכיום מזוהה עמו באופן אמיץ, ומופיעה על בולים, שטרות, מטבעות, סמלים, ועוד. גלגולי הדיוקן מתחילים באמצע המאה ה-18, בתחריט עץ ונציאני המתעד ככל הנראה חכם בן הזמן אך יוחס לרמב"ם, ועוברים דרך חכמי תנועת ההשכלה, ובהם יצחק שמואל רג'יו, שדחפו להפצת דיוקנו של מי שהיה דמות מופת לתנועה זו. עם זאת, אין כל ראיה לכך שאכן כך נראה הרמב"ם, וישנם כמה מאפיינים בתמונה שאינם עולים בקנה אחד עם הידוע לנו מפסיקותיו. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
26 בינואר 2009	דיוקנו המפורסם של הרמב"ם תמונתו של הרמב"ם היא דיוקן מפורסם של הרמב"ם, שכיום מזוהה עמו באופן אמיץ, ומופיעה על בולים, שטרות, מטבעות, סמלים, ועוד. גלגולי הדיוקן מתחילים באמצע המאה ה-18, בתחריט עץ ונציאני המתעד ככל הנראה חכם בן הזמן אך יוחס לרמב"ם, ועוברים דרך חכמי תנועת ההשכלה, ובהם יצחק שמואל רג'יו, שדחפו להפצת דיוקנו של מי שהיה דמות מופת לתנועה זו. עם זאת, אין כל ראיה לכך שאכן כך נראה הרמב"ם, וישנם כמה מאפיינים בתמונה שאינם עולים בקנה אחד עם הידוע לנו מפסיקותיו. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
27 בינואר 2009	אלבטרוסיים הם משפחה של עופות ימיים מסדרת היסעוראים הכוללת את הגדולות שבציפורי הים. האלבטרוסים נפוצים בעיקר בימים ליד אנטארקטיקה ובצפון האוקיינוס השקט. הם אינם מצויים בצפון האוקיינוס האטלנטי, אף על פי ששרידי מאובנים מעידים שבעבר היו נפוצים גם שם. הם ידועים ביפי מעופם ובהדר מוטת כנפיהם הרחבה. האלבטרוסים הם בין הגדולים שבעופות המסוגלים לעוף. האלבטרוסים מיומנים מאוד בתעופה, והם משתמשים בטכניקות שונות לניצול מוטת כנפיהם וכוחם, כדי לגמוא בקלות מרחקים עצומים. תזונתם מבוססת על דיונונים, דגים וקריל שאותם הם צדים על ידי צלילה לאוקיינוס או סמוך לפני המים. האלבטרוסים מקננים במושבות גדולות השוכנות בדרך כלל באיים מרוחקים באוקיינוס, לעיתים לצד מינים אחרים של עופות ימיים. האלבטרוסים הם מונוגמיים. הקשר בין הזכר לנקבה מטופח במשך מספר שנים, וכולל מצגי חיזור דמויי ריקוד. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
28 בינואר 2009	אלבטרוסיים הם משפחה של עופות ימיים מסדרת היסעוראים הכוללת את הגדולות שבציפורי הים. האלבטרוסים נפוצים בעיקר בימים ליד אנטארקטיקה ובצפון האוקיינוס השקט. הם אינם מצויים בצפון האוקיינוס האטלנטי, אף על פי ששרידי מאובנים מעידים שבעבר היו נפוצים גם שם. הם ידועים ביפי מעופם ובהדר מוטת כנפיהם הרחבה. האלבטרוסים הם בין הגדולים שבעופות המסוגלים לעוף. האלבטרוסים מיומנים מאוד בתעופה, והם משתמשים בטכניקות שונות לניצול מוטת כנפיהם וכוחם, כדי לגמוא בקלות מרחקים עצומים. תזונתם מבוססת על דיונונים, דגים וקריל שאותם הם צדים על ידי צלילה לאוקיינוס או סמוך לפני המים. האלבטרוסים מקננים במושבות גדולות השוכנות בדרך כלל באיים מרוחקים באוקיינוס, לעיתים לצד מינים אחרים של עופות ימיים. האלבטרוסים הם מונוגמיים. הקשר בין הזכר לנקבה מטופח במשך מספר שנים, וכולל מצגי חיזור דמויי ריקוד. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
29 בינואר 2009	חור שחור עם דסקת ספיחה, ה"בולע" כוכב אחר חור שחור הוא עצם בעל שדה כבידה כה חזק עד ששום גוף, לרבות אור, אינו יכול להתנתק ממנו. אם ננסה לחשב את מהירות המילוט מהחור השחור, נמצא שהיא עוברת את מהירות האור. אף על פי שהחור השחור עצמו אינו מקרין (ומכאן מגיע שמו), תהליך קוונטי המכונה קרינת הוקינג גורם לפליטת קרינה וחלקיקים מהגבול החיצוני של החור השחור, הקרוי אופק אירועים. מסתו של החור השחור גדלה כאשר גוף חוצה את אופק האירועים מבחוץ פנימה, ומאידך, מסתו קטנה בעקבות קרינת הוקינג. קיימות שתי שאלות פתוחות מפורסמות הקשורות לחורים שחורים. ידוע כי מאחורי כל אופק אירועים נמצאת סינגולריות. השאלה הראשונה היא שאלת נכונותה של השערת הצנזורה הקוסמית, לפיה כל סינגולריות מוסתרת מאיתנו על ידי אופק אירועים. השאלה השנייה קשורה למציאת פתרון לפרדוקס המידע הנובע מכך שחורים שחורים "מתאדים" מבלי לאבד מידע. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
30 בינואר 2009	חור שחור עם דסקת ספיחה, ה"בולע" כוכב אחר חור שחור הוא עצם בעל שדה כבידה כה חזק עד ששום גוף, לרבות אור, אינו יכול להתנתק ממנו. אם ננסה לחשב את מהירות המילוט מהחור השחור, נמצא שהיא עוברת את מהירות האור. אף על פי שהחור השחור עצמו אינו מקרין (ומכאן מגיע שמו), תהליך קוונטי המכונה קרינת הוקינג גורם לפליטת קרינה וחלקיקים מהגבול החיצוני של החור השחור, הקרוי אופק אירועים. מסתו של החור השחור גדלה כאשר גוף חוצה את אופק האירועים מבחוץ פנימה, ומאידך, מסתו קטנה בעקבות קרינת הוקינג. קיימות שתי שאלות פתוחות מפורסמות הקשורות לחורים שחורים. ידוע כי מאחורי כל אופק אירועים נמצאת סינגולריות. השאלה הראשונה היא שאלת נכונותה של השערת הצנזורה הקוסמית, לפיה כל סינגולריות מוסתרת מאיתנו על ידי אופק אירועים. השאלה השנייה קשורה למציאת פתרון לפרדוקס המידע הנובע מכך שחורים שחורים "מתאדים" מבלי לאבד מידע. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה
31 בינואר 2009	חור שחור עם דסקת ספיחה, ה"בולע" כוכב אחר חור שחור הוא עצם בעל שדה כבידה כה חזק עד ששום גוף, לרבות אור, אינו יכול להתנתק ממנו. אם ננסה לחשב את מהירות המילוט מהחור השחור, נמצא שהיא עוברת את מהירות האור. אף על פי שהחור השחור עצמו אינו מקרין (ומכאן מגיע שמו), תהליך קוונטי המכונה קרינת הוקינג גורם לפליטת קרינה וחלקיקים מהגבול החיצוני של החור השחור, הקרוי אופק אירועים. מסתו של החור השחור גדלה כאשר גוף חוצה את אופק האירועים מבחוץ פנימה, ומאידך, מסתו קטנה בעקבות קרינת הוקינג. קיימות שתי שאלות פתוחות מפורסמות הקשורות לחורים שחורים. ידוע כי מאחורי כל אופק אירועים נמצאת סינגולריות. השאלה הראשונה היא שאלת נכונותה של השערת הצנזורה הקוסמית, לפיה כל סינגולריות מוסתרת מאיתנו על ידי אופק אירועים. השאלה השנייה קשורה למציאת פתרון לפרדוקס המידע הנובע מכך שחורים שחורים "מתאדים" מבלי לאבד מידע. לערך המלא – מומלצים נוספים	עריכה - תבנית - שיחה